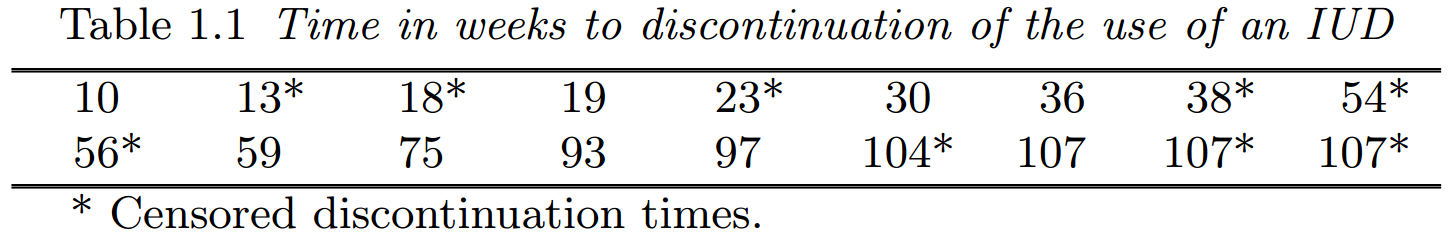R语言绘制生存分析曲线·从概念到实战的保姆级教程

大家好，欢迎来到IT知识分享网。

小罗碎碎念

生存分析 (survival analysis) 是一种分析数据的术语，该数据以时间为形式，用于描述从定义明确的时间起点 (time origin) 到某个特定事件或终点的发生。

在医学研究中，时间起点通常对应于将个体招募到实验研究中，例如比较两种或多种治疗的临床试验。这又可能与特定疾病的诊断、治疗方案的开始或某些不良事件的发生相吻合。如果终点是患者的死亡，那么得出的数据就是实际的生存时间。然而，当终点不是致命的，例如疼痛减轻或症状复发时，也可以获得类似形式的数据。

为了帮助大家更好的理解这一块的内容，小罗特意整理本篇推文，首先梳理生存分析的概念，随后便会利用RStudio手把手教大家如何绘制生存曲线。放心，看完这篇文章，你一定能彻底掌握生存分析！！

一、生存分析的应用

本篇推文的研究重点是生物医学中事件发生时间 (time-to-event) 数据的分析，在生物医学中，生存分析这一术语被广泛使用，即使终点不是死亡。然而，同样的技术也可用于许多其他应用领域，在这些领域中，它们被不同地称为事件历史分析 (event history analysis)、持续时间分析 (duration analysis)、转移分析 (transition analysis)、可靠性分析 (reliability analysis) 或失效时间建模 (failure-time modelling) 。

在犯罪学中

获释的囚犯可能会继续犯罪，从获释到随后犯罪的时间就是生存时间。这里，由于可能犯下的罪行不同，可能存在多种终点。对不同罪行发生时间及其影响因素的比较，将有助于对释放到社区的罪犯进行辅导。该领域的其他应用还包括犯罪生涯的持续时间、从犯罪到随后被捕的时间以及假释的持续时间。

在工程学中

从器械（如洗碗机或洗衣机）出现机械问题到该器械再次正常工作的这段时间，对于维护客户满意度至关重要。有些物品可能无法修复，因此无法记录修复时间。同时，调查与维修时间相关的因素也很重要，比如物品的使用年限、使用程度以及保养状况等。

在实验性农业中

种子发芽的时间、植物发病的时间以及农作物收获的时间都是事件发生时间。通常有很多因素可能会影响这些持续时间，确定最重要的因素将使实践得以完善。

例如，用除草剂处理一块土地后，化学品首次出现效果的时间就是生存时间，影响这一时间的因素可能有助于确定产品的特性。此时，很难记录除草剂出现效果的确切时间，只有在一定的时间段内才能知道是否产生了效果。

在金融领域

从提交申请到获得批准，处理抵押贷款申请所需的时间产生了事件发生时间的数据。有些申请没有进行到终点，可能是因为房屋销售失败，或者申请人安排了其他资金来源。然而，这也可能是因为申请流程已经花费了很长时间，因此必须考虑这些因撤销申请而删失 (censored) 的时间。

同样，一家公司偿还贷款所花费的时间也会产生生存数据，其中因贷款违约而产生的删失时间也包含在内。信贷公司可能非常关心诸如公司规模、年龄以及贷款规模等因素如何影响还款时间。

在人力资源领域

雇主可能会调查在特定时间段内开始工作的员工的在职时长。在分析时，许多员工可能仍在工作，因此他们只能提供关于在职时间的部分信息。特别令人感兴趣的是影响在职期的因素，如初始工资、工资涨幅、员工的资质等。

填补招聘职位所需的时间或首次晋升所需的时间都是该领域生存时间的进一步实例。在大型组织的不同部门之间，对这些事件发生时间的比较可能特别有助于识别好的管理规范。

在市场营销领域

客户流失率是一个重要的业务指标，它指的是在特定时间段内停用公司产品或服务的客户比例。之所以这一指标如此重要，很大程度上是因为获取新客户的成本往往远高于留住现有客户的成本。

生存分析在该领域有众多应用，例如客户离开公司的时间、取消服务协议的时间、升级产品（如 iPhone 或电脑）的时间，以及计算机软件或 iCloud 存储服务的订阅时长等。在所有这些情况下，客户流失的原因可能有很多，如服务不佳、产品质量低劣以及成本问题等。

流失时间还可能取决于一些其他因素，比如客户是否是通过其他客户推荐获得的、客户在客服电话上花费的时间以及是否有优惠活动可用等。对这些因素对客户留存时间的影响进行分析，有助于公司了解如何留住客户。

在政治学领域

在选举过程后组建政府的时间有时可能很短，但在其他情况下，各政党之间可能需要长时间的谈判。政府组建的延误可能会对政治或经济产生不利影响。研究相关因素，如参与谈判的政党数量、最大政党所占的多数席位以及各参与政党在意识形态上的冲突等，都有助于确定政府组建的时间。

此外，在政治学领域，事件发生时间分析的其他应用还包括政治生涯的长度、内阁政府的任期以及美国参议员的任期。在国际关系领域，战争的持续时间、贸易协定的期限以及政府的任期等，都适用于生存分析的方法。

在心理学领域

心理治疗疗程结束与行为发生临床显著变化之间的时间区间与潜在问题的治疗有关。

例如，在治疗酒精滥用问题时，识别与戒酒所需时间相关的因素至关重要。这些因素可能包括家族酒精依赖史、社会经济地位、个性问题、在就业保障和维持方面的困难，以及个体交往对象的吸烟和饮酒习惯。识别导致戒酒的因素可能有助于相关患者的管理。

本次讨论的重点是生存分析在医学研究数据中的应用，因此，大部分一般性讨论将以个体患者从进入研究到死亡或其他终点的生存时间来表述。

二、生存数据的特殊特征

我们必须首先考虑为什么生存数据不适用于数据分析中使用的标准统计程序。其中一个原因是生存数据通常不是对称分布的。

通常，由一组相似个体的生存时间构建的直方图会倾向于正偏态分布，也就是说，直方图在包含最多观测的区间的右侧会有一个较长的“尾巴”。因此，假设这类数据具有正态分布是不合理的。这个问题可以通过首先对数据进行转换以获得更对称的分布来解决，例如取对数。然而，更好的方法是采用其他分布。

生存数据的主要特征是生存时间经常是删失的 (censored)，这使得标准方法不适用。

2-1：删失

个体的生存时间称为删失，是指对该个体而言，感兴趣的终点尚未观察到。这可能是因为研究的数据要在一些人还活着的时候进行分析。或者在分析时个体的生存状态可能未知，因为该个体已经失访 (lost to follow-up)。

例如，假设某患者在被招募参加临床试验后，搬到国内的另一个地区或另一个国家，无法再追踪到。关于该患者的生存经历，唯一可获得的信息是他或她最后一次被确认存活的日期。这个日期可能是患者最后一次到诊所进行常规检查的日期。

当已知死亡原因与治疗无关时，实际的生存时间也可视为删失。然而，很难确定患者的死亡是否与他正在接受的特定治疗有关。例如，考虑一位参加前列腺癌替代疗法临床试验的患者，他遭遇了致命的交通事故。这场事故可能是由于眩晕发作导致的，而眩晕可能是分配给该患者的治疗方案的副作用。如果是这样的话，那么死亡就与治疗有关。在这种情况下，所有原因导致的死亡的生存时间，或患者正在接受治疗的主要疾病以外的其他原因导致的死亡时间，也可能需要进行生存分析。

在每种情况下，在时间 t0 进入研究的患者在时间 t0+t 死亡。然而，t 是未知的，要么是因为此人还活着，要么是由于他或她已失访。如果个体最后的已知生存时间为 t0+c，则时间 c 称为删失生存时间 (censored survival time). 这种删失发生在个体进入研究之后，即最后已知生存时间的右侧，因此称为右删失 (right censoring). 右删失生存时间小于实际但未知的生存时间。研究观察期结束时发生的右删失通常称为行政删失 (administrative censoring).

另一种形式的审查是左删失 (left censoring)，当个体的实际生存时间小于观测时间时就会遇到这种情况。考虑一项研究以说明这种形式的删失，该研究的兴趣集中在手术切除原发肿瘤后特定癌症的复发时间。术后三个月对患者进行检查以确定癌症是否复发，这时可能会发现部分患者出现了复发。对于此类患者，实际复发时间不到三个月，这些患者的复发时间是左删失。左删失的发生率远低于右删失，因此本次重点将放在右删失生存数据的分析中。

另一种类型的删失是区间删失 (interval censoring). 此时，已知个体在一段时间内经历过某个事件。再次考虑上述左删失讨论中使用的有关肿瘤复发时间的例子。如果患者在三个月后观察到疾病已痊愈，但在术后六个月检查时发现疾病复发，则该患者的实际复发时间在三个月至六个月之间。观测复发时间称为区间删失。

2-2：独立删失

在分析删失的生存数据时，一个重要的假设是，个体的实际生存时间 t 不依赖于任何导致该个体的生存时间在时间 c 删失的机制，其中 c<t。这种类型的删失称为独立删失或非信息性删失 (independent or non-informative censoring).

这意味着，如果我们考虑一组具有相同相关预后变量值的个体，则生存时间在时间 c 处删失的个体必须代表该组中生存到该时间的所有其他个体。如果删失过程随机进行，则生存时间删失的患者将代表删失时处于风险中的患者。

类似地，当要在日历时间中的预定点或在每个患者的时间起点之后的固定时间区间分析生存数据时，仍然活着的个体的预后可视为与删失独立，只要在检查数据之前指定分析时间即可。然而，如果个体的生存时间因身体状况恶化而停止治疗导致删失，则不能做出这一假设。此类删失称为相依删失或信息性删失 (dependent or informative censoring).

2-3：研究时间和患者时间

在典型的研究中，患者并非都在同一时间招募，而是在数月甚至数年的时间内陆续招募。招募完成后，将对患者进行跟踪调查，直至其去世，或者直至研究结束，此时将分析数据。尽管可以观察到一些患者的实际生存时间，但一些患者可能会在招募后失去联系，而其他患者在研究结束时可能仍然健在。个体参与研究的时间段称为研究时间 (study time).

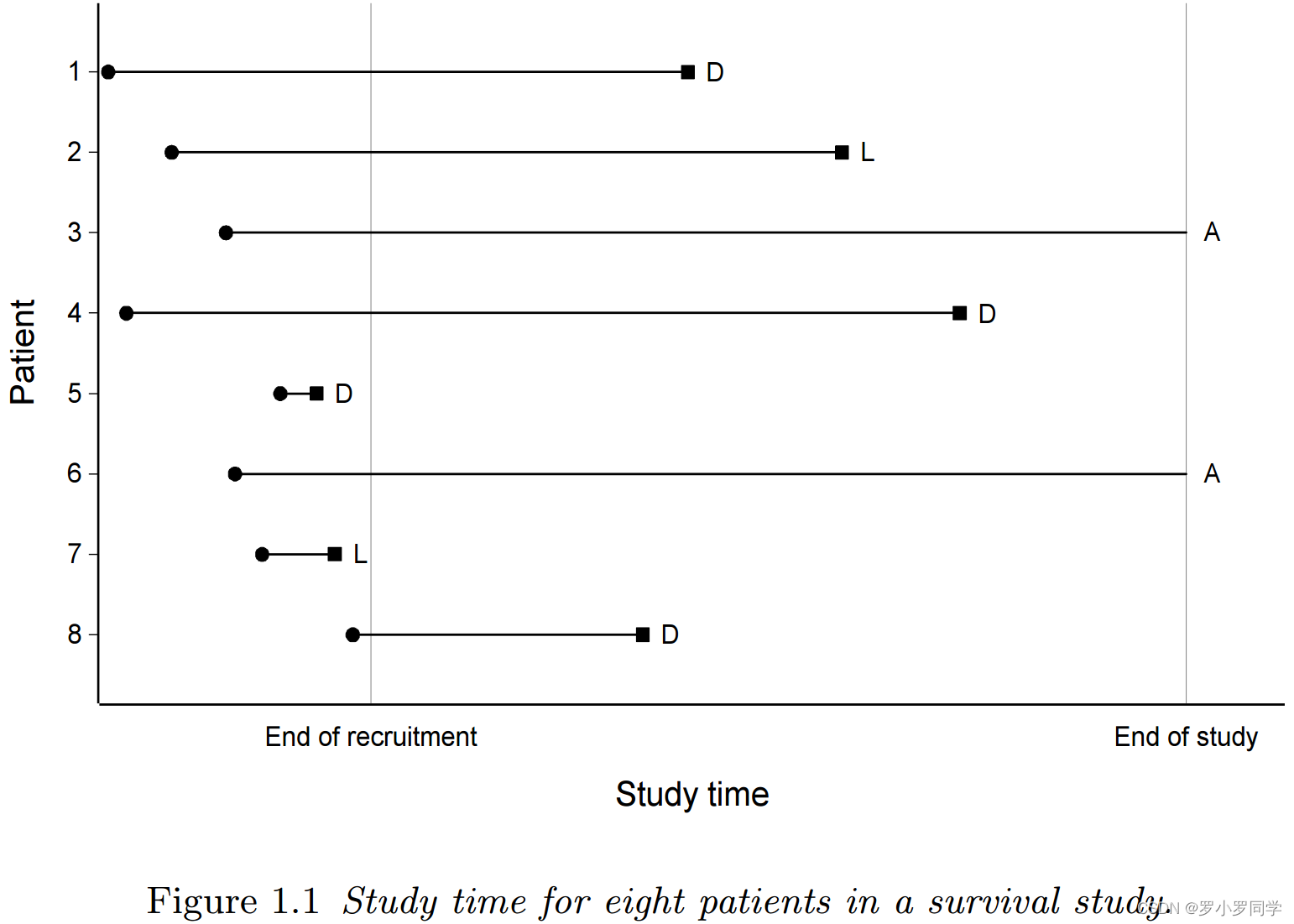
临床试验中八个人的研究时间如图 1.1 所示，其中进入研究的时间用“•”表示。该图显示，个体 1, 4, 5 和 8 在研究过程中死亡 (D)，个体 2 和 7 失访 (L)，个体 3 和 6 在观察期结束时仍然活着 (A).

图 1.1

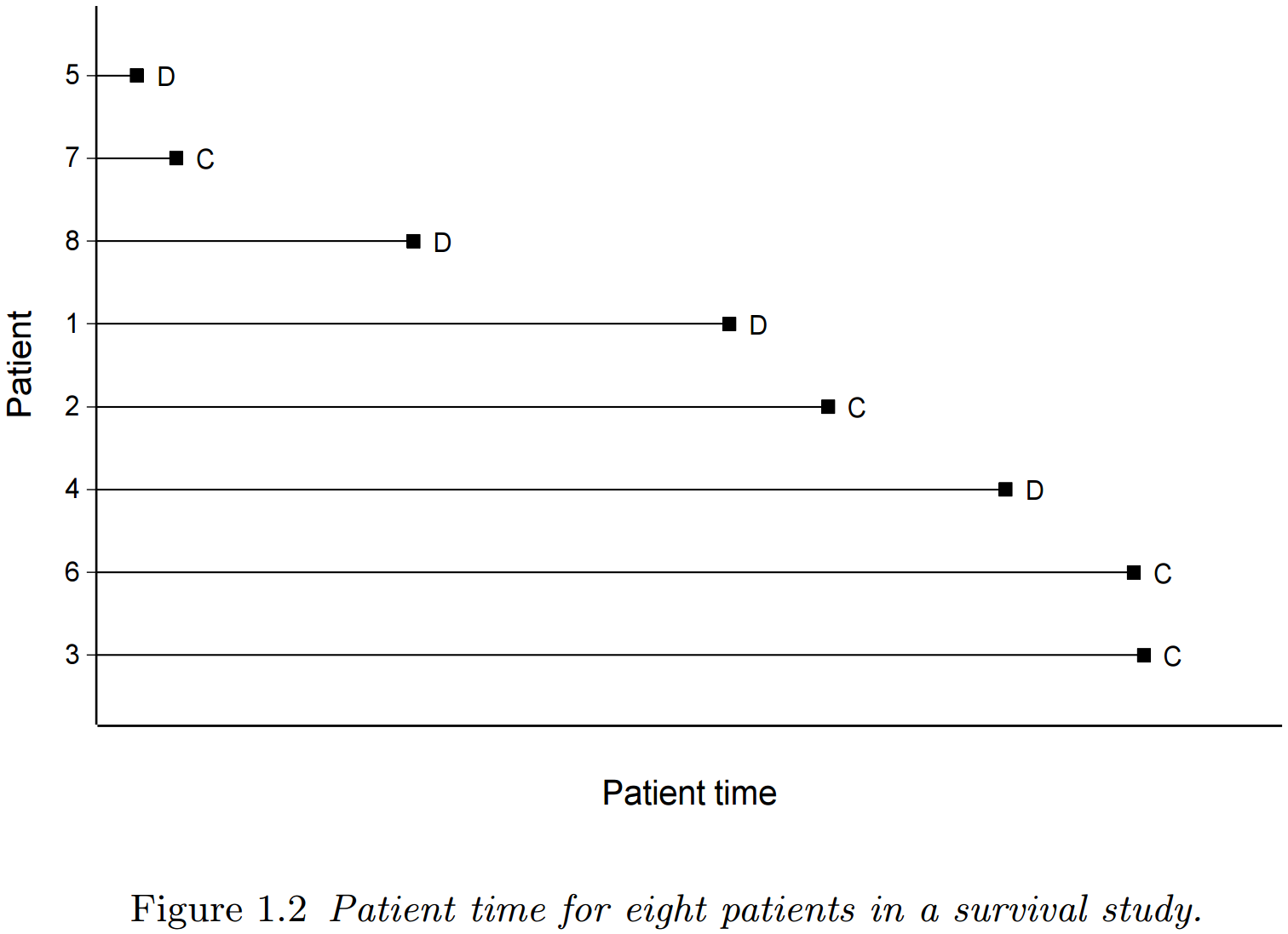
就每个患者而言，试验在 t0 开始。图 1.1 所示的八个个体的相应生存时间如图 1.2 所示。患者在研究中经历的时间段，从其时间起点开始测量，通常称为患者时间 (patient time). 从时间起点到患者死亡 (D) 的时间段即为生存时间，这是为个体 1, 4, 5 和 8 记录的。剩余个体的生存时间是右删失的 ©.

图 1.2

在实践中，记录的实际数据将是每个个体进入研究的日期，以及每个个体死亡或最后已知存活的日期。然后可以计算生存时间，以天、周或月为单位，以最合适的为准。大多数用于生存分析的计算机软件包都可以根据日期形式的数据执行此类计算。

2-4：一些示例

示例 1.1 (停用宫内节育器的时间)

在涉及避孕措施的试验中，预防怀孕是评估可接受性的一个明显标准。然而，现代避孕措施的失败率非常低，因此，诸如闭经（长期无出血）、不规则或延长出血等出血障碍的发生情况，在评估某种避孕方法时变得尤为重要。

为了推动对分析避孕试验中女性月经出血数据方法的研究，世界卫生组织提供了涉及多种不同类型避孕方法的临床试验数据 (WHO, 1987). 这些数据集的一部分涉及女性开始使用某种避孕方法到停用该方法的时间，如果已知停用原因，则记录停用原因。

表 1.1 中的数据指的是从开始使用一种特定类型的宫内节育器 (intrauterine device, IUD)，称为 Multiload 250，到因月经出血问题而停用该设备所经历的周数。这些数据来自 18 名女性，她们的年龄都在 18 至 35 岁之间，且都有过两次怀孕经历。删失的停用时间用星号标记。

在此示例中，时间起点对应于女性使用宫内节育器的第一天，终点是因出血问题导致的停用。研究中的一些女性因为想要怀孕或不再需要避孕药而停用宫内节育器，而其他女性则只是失访。这些原因导致了 13, 18, 23, 38, 54 和 56 周的删失停用时间。该研究方案要求记录每位女性的月经出血经历，为期两年。出于实际原因，每个女性在招募后两年内都无法接受检查以确定她们是否仍在使用宫内节育器，这就是为什么有 3 个停用时间大于 104 周的右删失时间。

分析这些数据的一个目的是总结停用时间的分布。然后我们可能希望估计停用宫内节育器的中位时间，或者估计女性在特定时间段后停用该设备的概率。事实上，以时间为函数的这种估计概率图将为数据提供一个有用的总结。

示例 1.2 (患乳腺癌妇女的预后)

乳腺癌是西方国家女性最常见的癌症形式之一。然而，肿瘤的生物学行为往往难以预测，许多研究集中在肿瘤是否可能已经转移或扩散到身体的其他器官。大约 80% 的原发性乳腺癌女性患者可能患有已经转移到其他部位的肿瘤。如果能确定这些患者，可以针对她们进行辅助治疗，而剩下的 20% 可以通过手术治愈。

Middlesex Hospital 开展了一项调查，相关记录可见 Leathem and Brooks (1987). 该调查旨在评估一种组织化学标志物，用以区分已经发生转移和未发生转移的原发性乳腺癌。研究中的标志物是一种来自罗马蜗牛 Helix pomatia 的白蛋白腺凝集素，即 Helix pomatia agglutinin (HPA). 这种标志物与发生局部淋巴结转移的乳腺癌细胞结合，而经 HPA 染色的细胞可以通过显微镜检查来识别。

为了探究 HPA 染色是否可用于预测罹患乳腺癌女性的生存状况，研究者开展了一项回顾性研究，研究对象为接受乳腺癌手术治疗的女性的病历记录。对这些女性的肿瘤切片进行 HPA 处理，随后将每个肿瘤分为阳性染色和阴性染色，其中阳性染色表示肿瘤具有转移潜力。

该研究于 1987 年 7 月结束，此时计算了死于乳腺癌的女性的生存时间。对于 1987 年 7 月时生存状态未知的女性，从手术日期到她们最后一次被确认存活的日期之间的时间视为删失生存时间。死于乳腺癌以外原因的女性的生存时间也视为右删失。

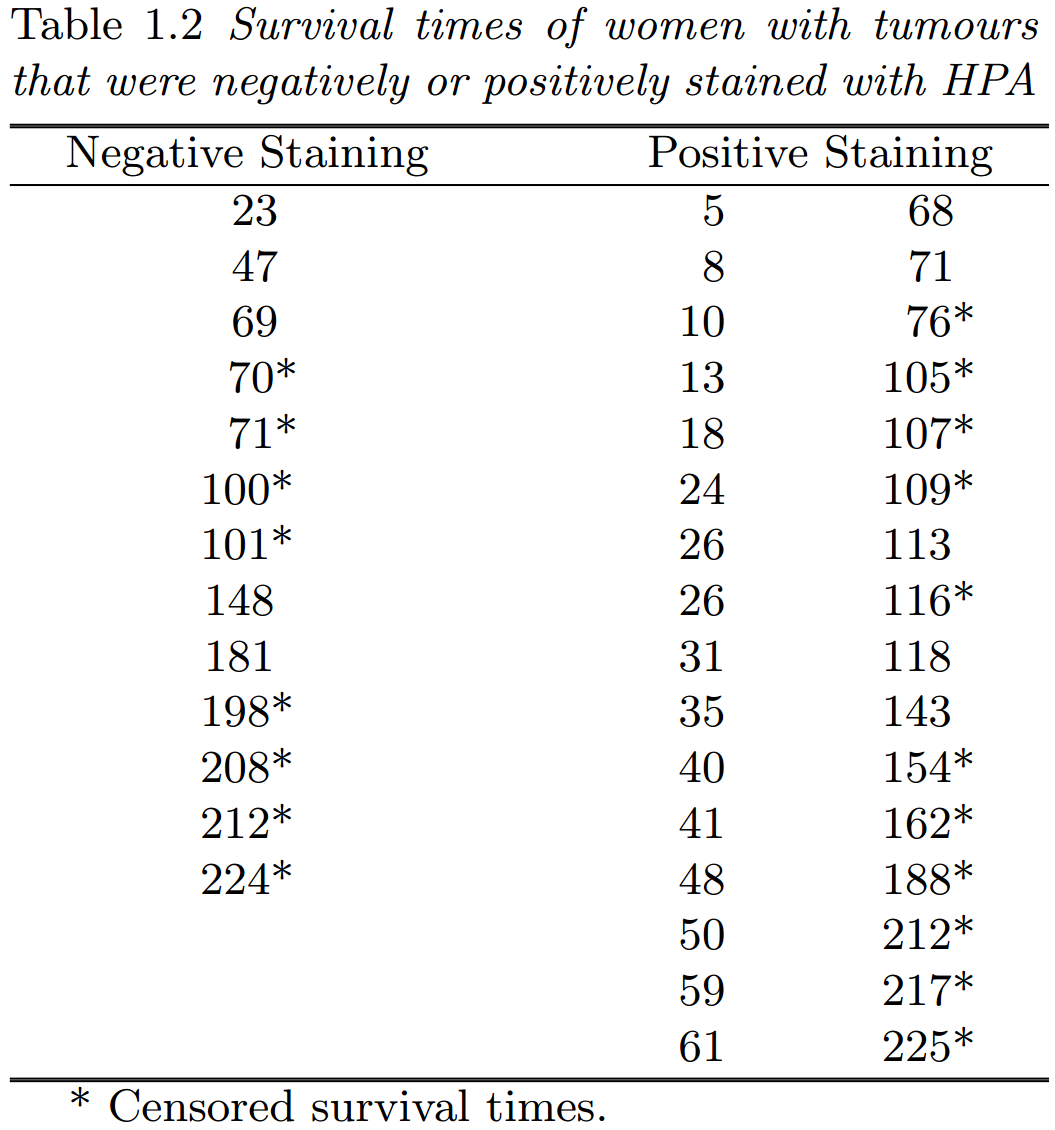
表 1.2 中的数据指的是 1969 年 1 月至 1971 年 12 月期间接受单纯或根治性乳房切除术治疗的 II 级、III 级或 IV 级肿瘤的女性的生存月数。在表中，每位女性的生存时间根据其肿瘤是否为阳性染色进行分类。

在分析这项研究的数据时，我们特别感兴趣的是，这两组女性的生存经历是否存在差异。如果有证据表明，那些 HPA 染色阴性的女性在术后往往比那些染色阳性的女性活得更长，我们将得出结论，癌症患者的预后取决于染色程序的结果。

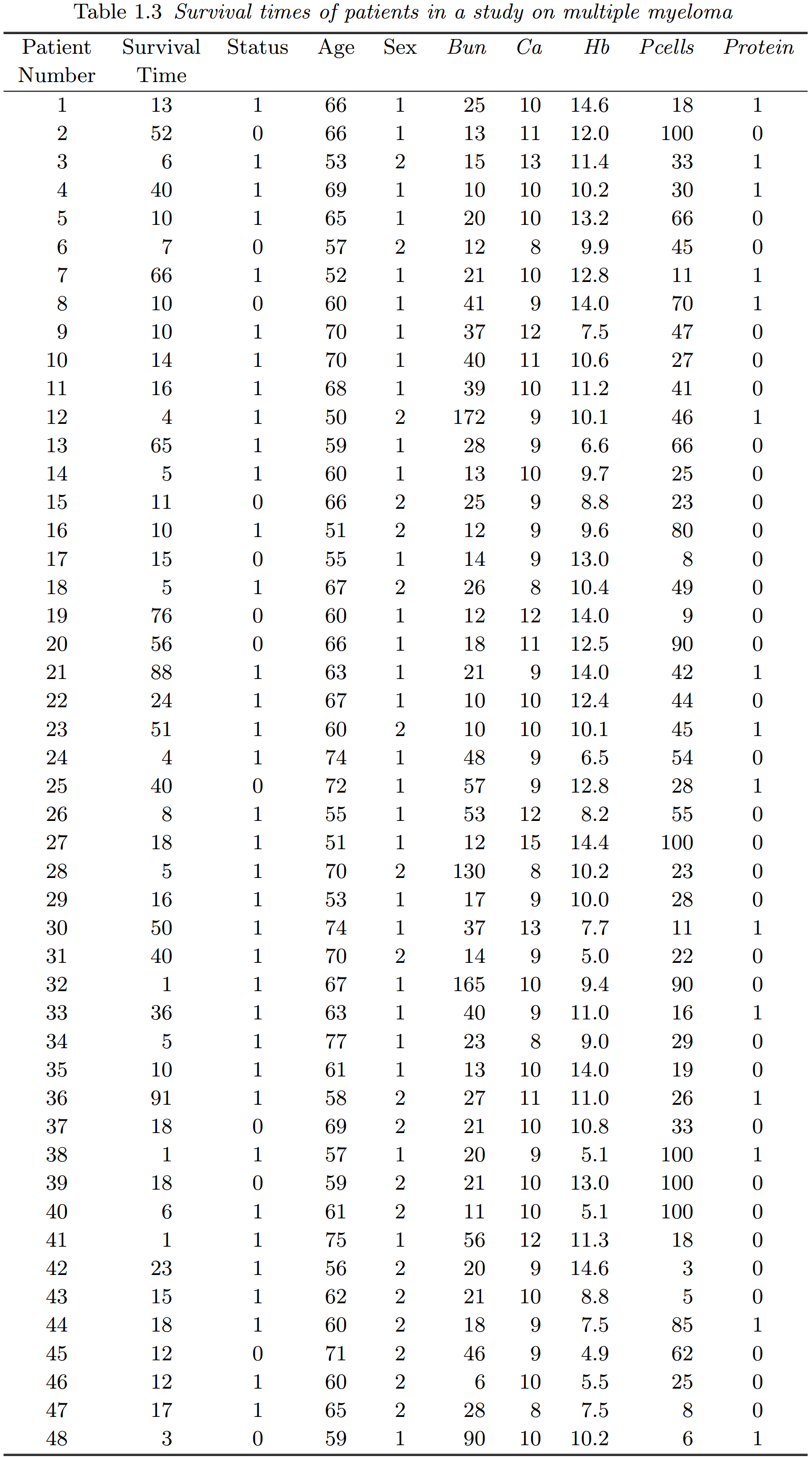
示例 1.3 (多发性骨髓瘤患者的生存率)

多发性骨髓瘤是一种恶性疾病，其特征是异常浆细胞（一种白细胞）在骨髓中积聚。骨内异常浆细胞的增殖导致疼痛和骨组织的破坏。多发性骨髓瘤患者也会出现贫血、出血、反复感染和虚弱。这种情况总是致命的，除非接受治疗。

Medical Center of the University of West Virginia, USA 进行了一项研究，其目的是检验某些解释变量或协变量的值与患者生存时间之间的关系。在这项研究中，主要响应变量是多发性骨髓瘤从诊断到死亡的时间，以月为单位。

表 1.3 中的数据来自 Krall, Uthoff and Harley (1975)，涉及 48 名患者，他们的年龄都在 50 至 80 岁之间。到研究完成时，部分患者还未死亡，因此他们的生存时间是右删失的。表中个体生存状态的编码规则为：0 表示删失观测，1 表示多发性骨髓瘤死亡。

在诊断时，记录了每位患者的许多解释变量的值。这些包括患者的年龄（岁）、性别（1 = 男性，2 = 女性）、血尿素氮 (Bun) 水平、血清钙 (Ca)、血红蛋白 (Hb)、骨髓中血浆细胞的百分比 (Pcells) 和一个指示变量 (Protein)，用于指示尿液中是否存在 Bence-Jones 蛋白（0 = 不存在，1 = 存在）。

分析这些数据的主要目的是研究风险因素 Bun, Ca, Hb, Pcells 和 Protein 对多发性骨髓瘤患者生存时间的影响。这些风险因素的影响可能会因患者的年龄或性别而改变，因此，还需要研究生存时间与重要风险因素之间的关系在每个性别以及不同年龄组中的一致性程度。

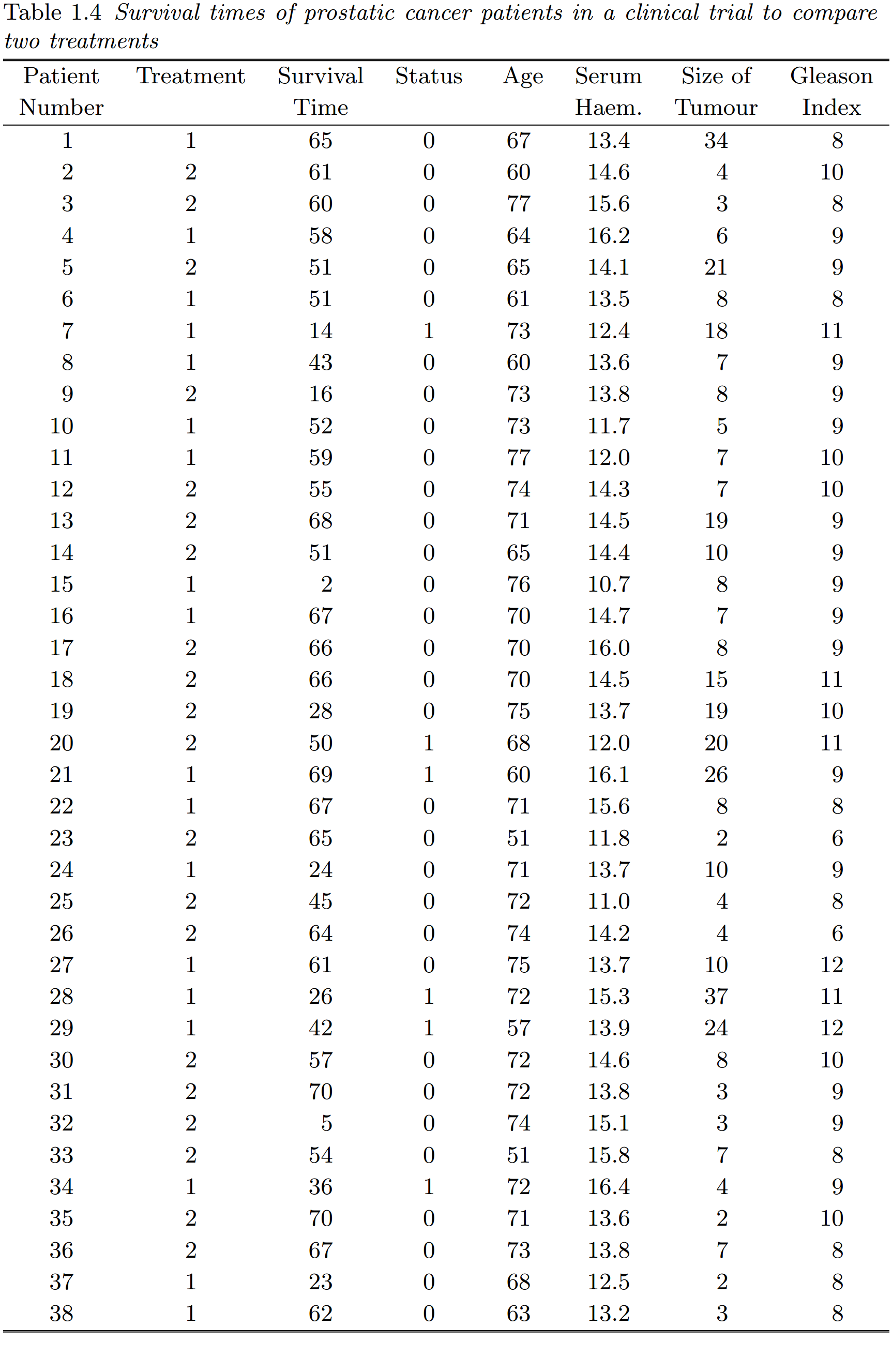
示例 1.4 (前列腺癌两种疗法的比较)

1967年，Veteran’s Administration Cooperative Urological Research Group 开始了一项随机对照临床试验，以比较前列腺癌的疗法。该试验是双盲的，研究中使用的两种疗法是安慰剂和 1.0 毫克己烯雌酚 (DES)。每天口服治疗。研究的时间起点是患者被随机分配接受治疗的日期，终点是患者死于前列腺癌的日期。

完整的数据集在 Andrews and Herzberg (1985) 中给出，但本例中使用的数据来自患有 III 期癌症的患者，即有证据表明这些患者的肿瘤局部扩展至前列腺包膜之外，但血清前列腺酸性磷酸酶未升高。此外，这些患者没有心血管病史，在试验开始时心电图结果正常，白天没有卧床休息。

除了记录研究中每个患者的生存时间外，还记录了许多其他预后因素的信息。其中包括患者进入试验时的年龄、他们的血清血红蛋白水平（单位：g/100 ml）、原发肿瘤大小（单位：cm²）以及肿瘤分期和分级的综合指数值。这个指数称为 Gleason 指数；越晚期，该指数的值就越大。

表 1.4 给出了 38 名患者的记录数据，其中生存时间以月为单位。因其他原因死亡或失访的患者的生存时间视为删失。研究结束时，若患者死于前列腺癌，则与个体状态相关的变量的值为 1，若生存时间删失，则为 0。当个体接受 DES 治疗时，与治疗组别相关的变量取值为 2，而当个体接受安慰剂治疗时，变量取值为 1.

本研究的主要目的是确定是否有证据表明接受 DES 治疗的患者比接受安慰剂治疗的患者生存时间更长。

由于本例所依据的数据来自一项随机试验，人们可能会期望两组治疗患者中预后因素（即患者年龄、血清血红蛋白水平、肿瘤大小和 Gleason 指数）的分布是相似的。然而，依赖这一假设并不明智。例如，结果表明安慰剂组患者的肿瘤平均大小可能大于接受 DES 治疗的患者。如果大肿瘤患者的预后比小肿瘤患者差，那么治疗效果就会被高估，除非在分析中充分考虑肿瘤的大小。因此，首先有必要确定是否有任何协变量与生存时间相关。若如此，在比较两个治疗组患者的生存时间时，需要考虑这些变量的效应。

三、生存函数，风险函数和累积风险函数

在总结生存数据时，主要关注三个函数，即生存函数 (survival or survivor function)、风险函数 (hazard function) 和累积风险函数 (cumulative hazard function)。

3-1：生存函数

个体的实际生存时间 t 可以视为变量 T 的观测，其中 T 可以取任意非负值。T 可取的值具有概率分布，我们将 T 称为与生存时间相关的随机变量。

生存函数 S(t) 定义为生存时间大于等于 t 的概率，因此根据式 (1.1)
$\begin{equation} S(t)=\text{P}(T\geqslant t)=1-F(t) \tag{1.2} \end{equation}$
因此，生存函数可以用来表示一个个体在任何给定时间之后生存的概率。

3-2：风险函数

风险函数 (hazard function) 广泛用于表示某个时间 t 发生的事件（如死亡）的风险或危险 (hazard or risk)。该函数是从一个个体在时间 t 死亡的概率中获得的，前提是这个个体已经生存到了这个时间。

根据式 (1.3) 中风险函数的定义，h(t) 是时间 t 处的事件率，前提是事件在 t 之前没有发生。具体而言，如果生存时间以天为单位，h(t) 是在第 t 天开始时有事件发生风险的个体在该天经历事件的近似概率。时间 t 的风险函数也可以视为个体在单位时间内经历的预期事件数，假设在此之前没有发生过事件，并假设风险在该时间段内是恒定的。

根据式 (1.3) 中风险函数的定义，生存函数和风险函数之间存在一些有用的关系。根据概率论，以事件 B 的发生为条件，事件 A 的概率由 P(A|B)=P(AB)/P(B) 给出，其中 P(AB) 是 A 和 B 共同发生的概率。使用该关系，式 (1.3) 风险函数定义中的条件概率

$\begin{aligned}\frac{\mathrm{P}(t\leqslant T<t+\delta t)}{\mathrm{P}(T\geqslant t)}\end{aligned}$
等于

$\begin{aligned}\frac{F(t+\delta t)-F(t)}{S(t)}\end{aligned}$
其中 F(t) 为 T 的分布函数。那么

$h(t)=\lim_{\delta t\to0}\left\{\frac{F(t+\delta t)-F(t)}{\delta t}\right\}\frac{1}{S(t)}$
现在

$\lim_{\delta t\to0}\left\{\frac{F(t+\delta t)-F(t)}{\delta t}\right\}$
是 F(t) 关于 t 的导数的定义式，也就是 f(t)，因此

$\begin{equation} h(t)=\frac{f(t)}{S(t)} \tag{1.4} \end{equation}$
总之，式 (1.1), (1.2) 和 (1.4) 表明，利用 f(t),S(t),h(t) 中的任何一个可以确定其他两个。

3-3：累积风险函数

根据式 (1.4) 可以得出

$\begin{equation} h(t)=-\frac{\mathrm{d}}{\mathrm{d}t}\{\log S(t)\} \tag{1.5} \end{equation}$
因此

$\begin{equation} S(t)=\exp\left\{-H(t)\right\} \tag{1.6} \end{equation}$
其中

$\begin{equation} H(t)=\int_0^th(u)\mathrm{d}u \tag{1.7} \end{equation}$
函数 H(t) 在生存分析中作用广泛，称为集成或累积风险函数 (integrated or cumulative hazard function). 根据式 (1.6)，累积风险函数也可根据生存函数得到，因为

$\begin{equation} H(t)=-\log S(t) \tag{1.8} \end{equation}$
累积风险函数 H(t) 是直到时间 t 时发生事件的累积风险。如果事件是死亡，则 H(t) 总结了截至时间 t 的死亡风险，前提是死亡在 t 之前尚未发生。时间 t 处的累积风险函数也可解释为从时间起点到 t 的时间区间内发生事件的预期数量。

累积风险函数有可能大于 1. 使用式 (1.8)，当 −log⁡S(t)⩾1 即 S(t)⩽e−1=0.37 时，H(t)⩾1。当时间 t 之后发生事件的概率小于 0.37 时，累积风险大于 1，这意味着在时间区间 (0,t) 内预计会发生多个事件。因此生存函数 S(t) 可以更准确地定义为时间 t 之后发生一个或多个事件的概率。

四、Kaplan-Meier生存曲线绘制

生存分析研究的是某个事件发生之前过去的时间，在临床研究中最常见的应用就是死亡率的估计(预测患者的生存时间)，不过生存分析也可以应用于其他领域如机械故障时间等。

在R中，survival包中有很多函数可以对生存数据进行建模，可以使用survfit()函数来估计删失数据的生存曲线，使用coxph()函数用来拟合Cox比例风险模型。

在survminer包中，可以使用plot()函数、ggsurvplot()函数用来绘制Kaplan-Meier生存曲线。接下来重点介绍，如何在R中使用ggsurvplot()函数绘制Kaplan-Meier生存曲线。

4-1：安装和加载R包

绘制Kaplan-Meier生存曲线需要用到的R包：survminer和survival。

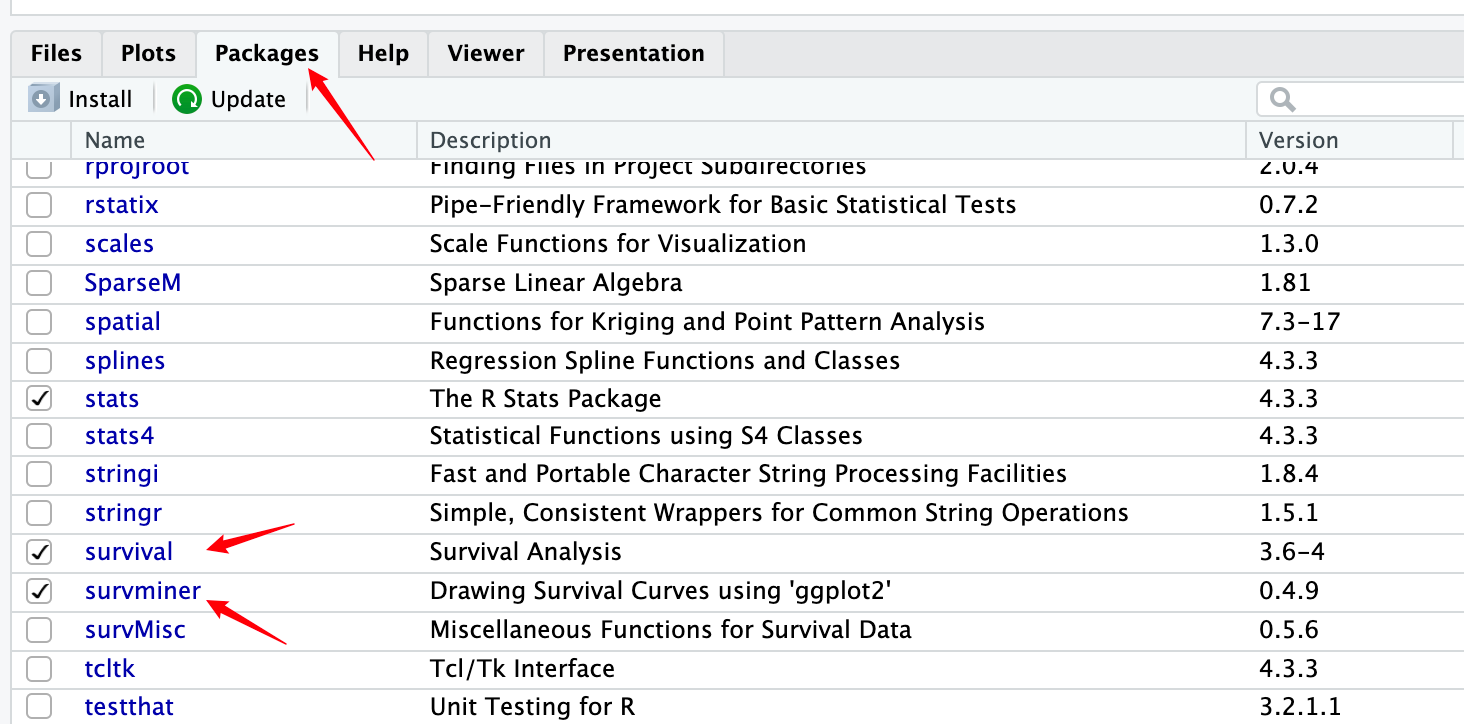
install.packages("survminer") # 安装survminer包 install.packages("survival") # 安装survival包 library(survminer) # 加载包 library(survival) # 加载包

⚠️要安装的依赖项目很多，请耐心等待，执行上述代码以后，会发现页面右侧的Packages界面出现了两个包，并且都被勾选上了。

4-2：导入内置数据集

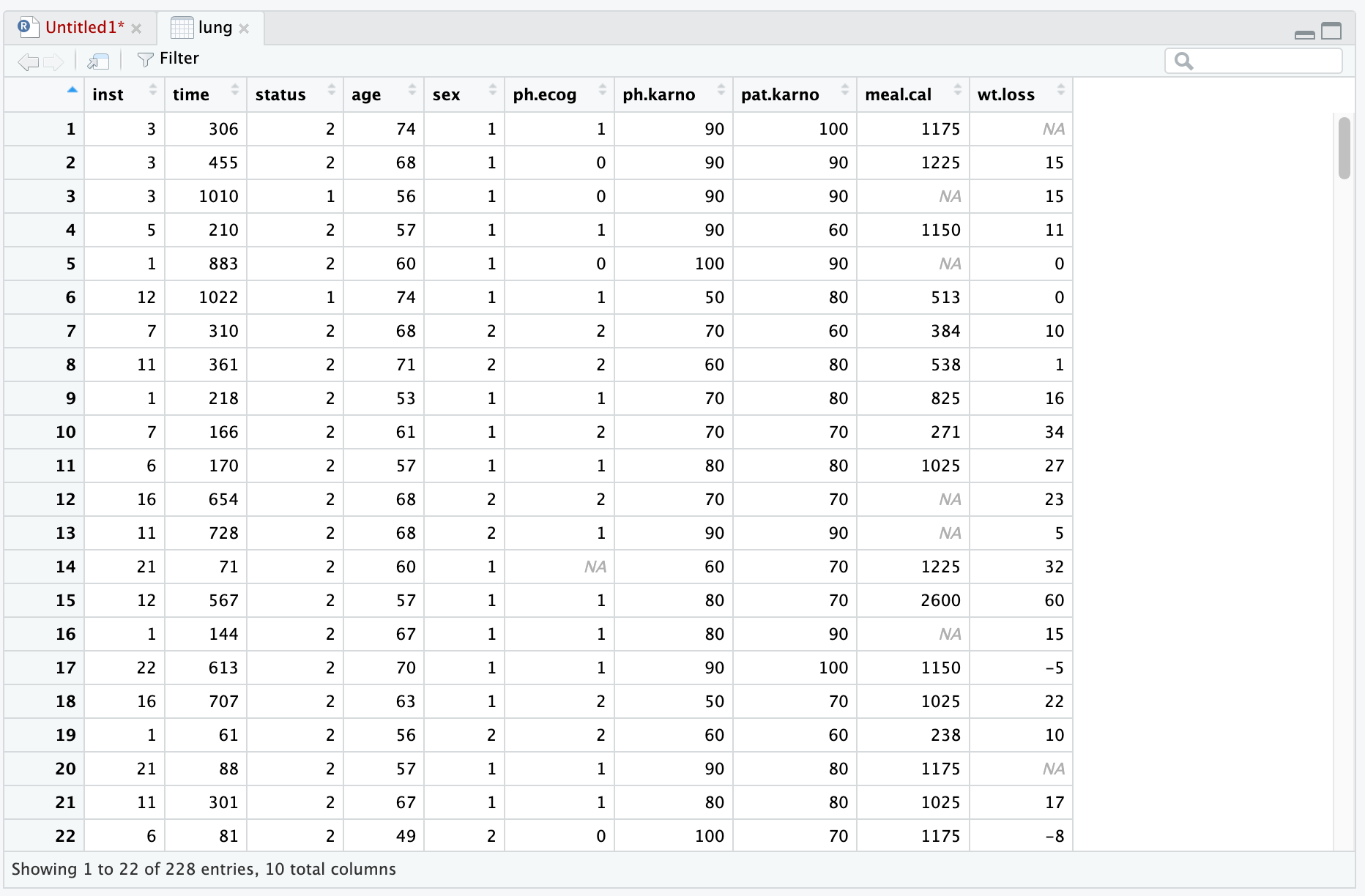
使用survival包的lung数据集进行演示。

data(lung) # 加载lung数据集 View(lung) # 查看数据集

⚠️：lung数据集：NCCTG晚期肺癌患者的生存率。

inst # 机构代码；
time # 生存天数；
status # 生存状态，1为删失，2为死亡；
age # 年龄；
sex # 性别，1为男性，2为女性；
ph.ecog、ph.karno、pat.karno # 为病人和患者评分，这里用不到；
meal.cal # 进食时消耗的卡路里；
wt.loss # 最近6个月内的体重下降。

4-3：拟合生存曲线

1、创建生存对象

在survival包中先使用Surv()函数创建生存对象，生存对象是将事件时间和删失信息合并在一起的数据结构。

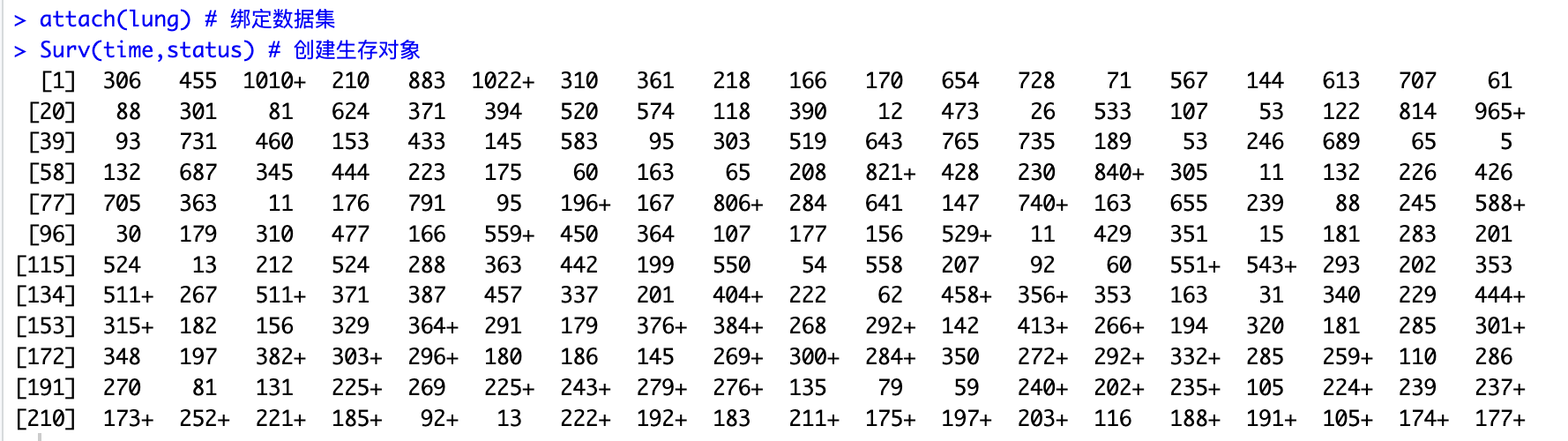
attach(lung) # 绑定数据集 Surv(time,status) # 创建生存对象

在生存分析中，attach() 和 Surv() 是R语言中用于处理生存数据的函数。

attach(lung)：这行代码的作用是将名为 lung 的数据集加载到R的搜索路径中。在R中，attach() 函数用于将数据框（data frame）中的数据绑定到当前的工作环境，使得可以直接访问数据框中的列而不需要通过数据框的名称来引用。
Surv(time, status)：这行代码使用 Surv() 函数创建了一个生存对象。在生存分析中，核心是创建一个表示生存时间（survival time）和生存状态（status）的对象。Surv() 函数需要两个参数：
- time：表示个体从开始观察到事件发生（如疾病复发、死亡等）的时间长度。
- status：一个二元变量，用来表示个体在观察结束时的状态。通常，status = 1 表示个体经历了感兴趣的事件（例如，死亡），而 status = 0 表示个体在观察结束时仍然存活（右删失）或者在其他非事件原因下失去了进一步的跟踪（截尾）。

这个生存对象通常用于后续的生存分析模型中，如Cox比例风险模型等，以估计生存函数、风险比或者进行时间至事件的分析。

需要注意的是，attach() 并不是加载数据集的最佳实践，特别是在大型项目或与其他R用户协作时，因为它可能导致作用域的混乱。更推荐使用如 library()、require() 或直接使用数据集名前缀的方式来访问数据集。此外，随着R语言的发展，Surv() 函数的使用也逐渐被 survival 包中的 Survival() 类型的对象所取代，后者提供了更丰富的功能和更清晰的语法结构。

在上面输出的生存对象中，带”+”号的表示右删失数据。

2、拟合曲线

在R语言中，生存分析通常涉及使用survival包中的survfit()函数来拟合生存数据。

fit <- survfit(Surv(time,status) ~ sex,data = lung) # 数据集来源 fit # 查看拟合曲线信息

fit <- survfit(Surv(time, status) ~ sex, data = lung)：这行代码执行了生存分析中的一个关键步骤，即拟合生存曲线。
- survfit()：这是survival包中的一个函数，用于拟合生存数据。它返回一个列表，其中包含了生存概率的估计值。
- Surv(time, status)：这是一个Surv对象，表示生存时间（time）和生存状态（status）。生存状态是一个指示器，表明个体是否经历了感兴趣的事件（如死亡，status = 1）或在观察结束时仍然存活（status = 0）。
- ~ sex：这是一个公式，表示生存曲线将根据性别（sex）进行分层或分组。这意味着模型将为每个性别拟合一个不同的生存曲线。
- data = lung：指定了包含生存数据的数据集，这里假设lung是一个数据框（data frame），其中包含了time、status和sex等变量。
- fit <-：在<-的左边是变量名fit，右边是survfit()函数的调用结果。这意味着拟合结果将被存储在名为fit的变量中。
fit：在R中，直接输入变量名并按下回车会打印该变量的内容。因此，这行代码的作用是输出fit变量的内容，即上面通过survfit()函数拟合的生存曲线信息。

当你运行fit，R会显示生存曲线拟合的结果，通常包括每个时间点的生存概率估计以及与分层因素（这里是sex）相关的统计信息。

这个拟合结果可以用于进一步分析，比如比较不同性别的生存曲线，或者绘制生存曲线图来直观展示生存概率随时间的变化。

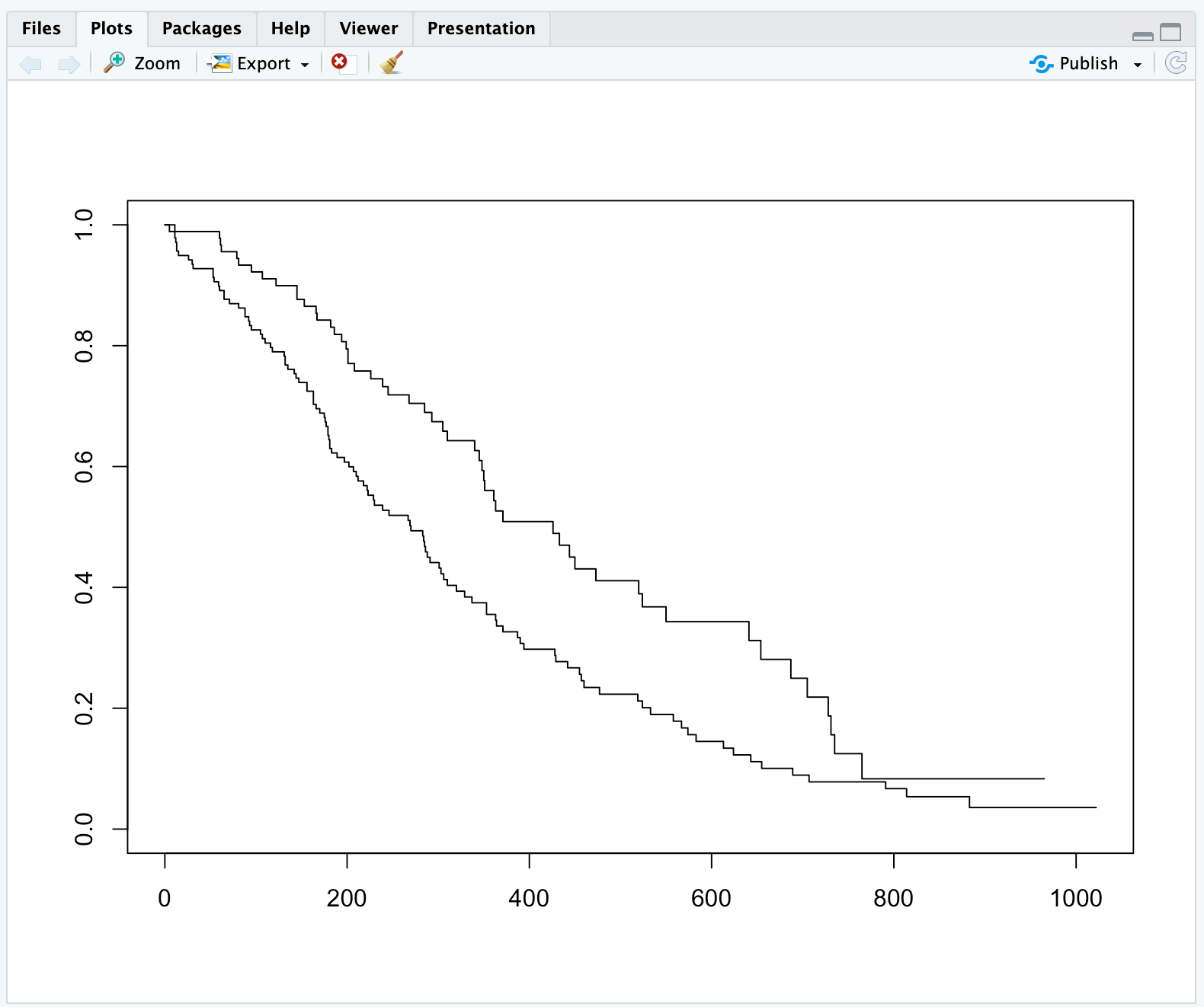
在R中，可以使用plot(fit)来生成生存曲线的图形表示。

从上图可知，lung数据集中男性138例，女性90例；男性和女性发生感兴趣结局事件分别有112例和53例。男性和女性的中位生存时间分别为270天和426天。

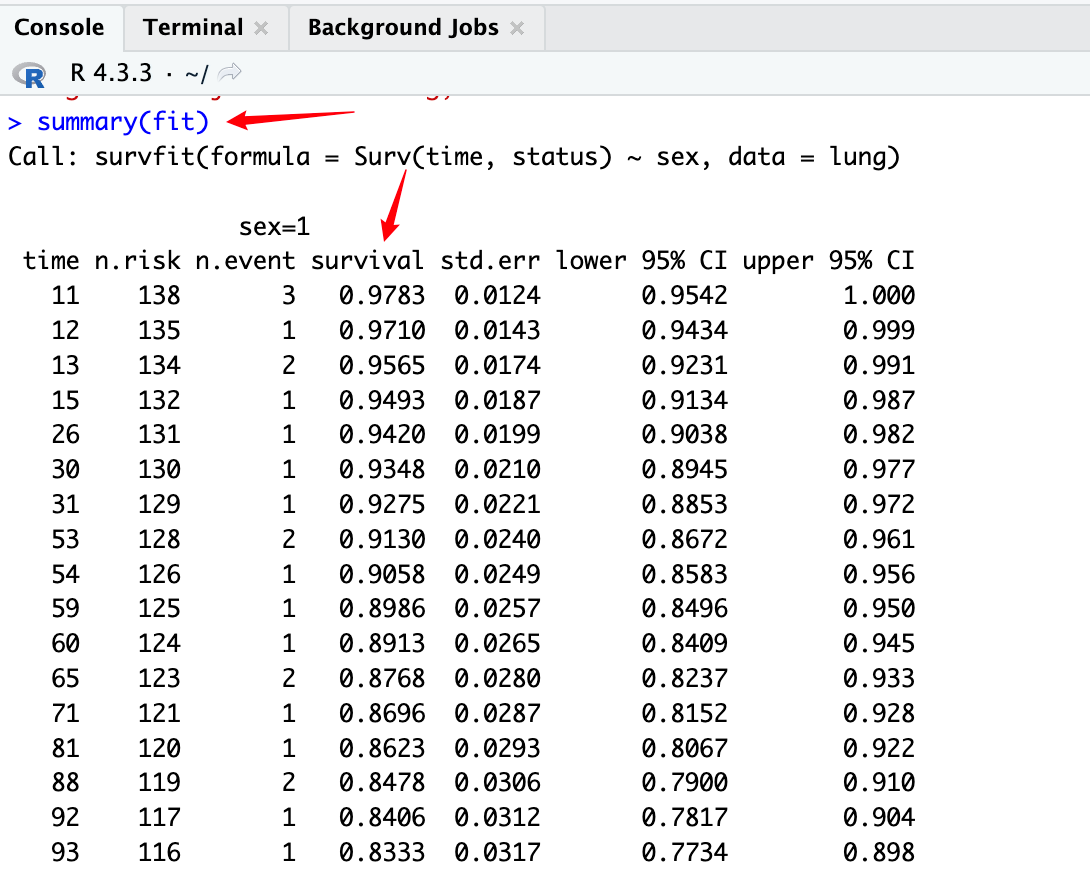
还可以使用summary()函数输出更多详细信息。

上图中survival为生存函数在生存时间点处的KM估计值。同时，输出结果中还给出了估计的标准误差和95%置信区间。

4-4：绘制基础曲线

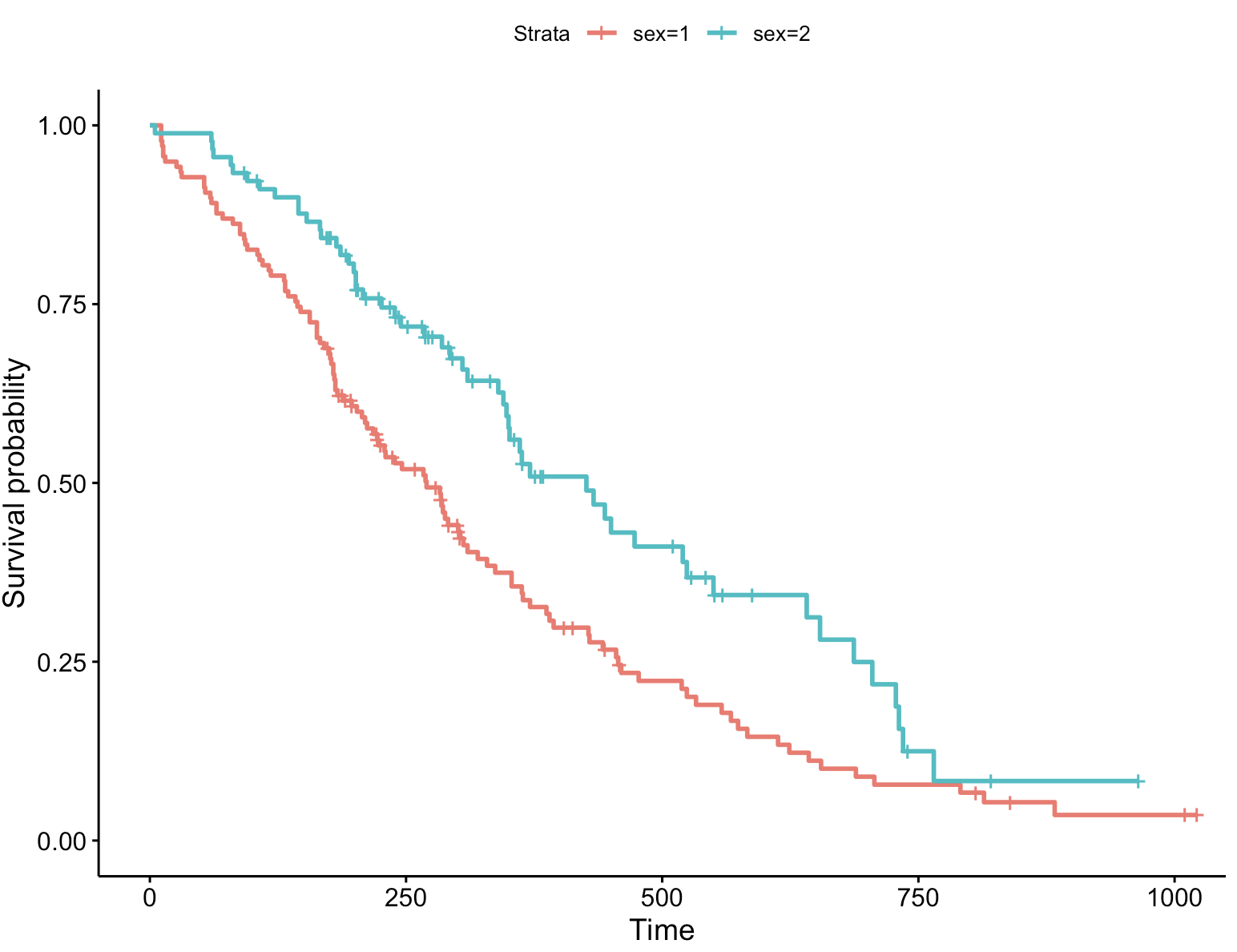
在R语言中，ggsurvplot() 函数是 survminer 包提供的一个用于绘制生存曲线的高级函数，它基于 ggplot2 包的图形语法。

ggsurvplot(fit, data = lung)

4-5：自定义曲线参数

1、增加中位生存时间

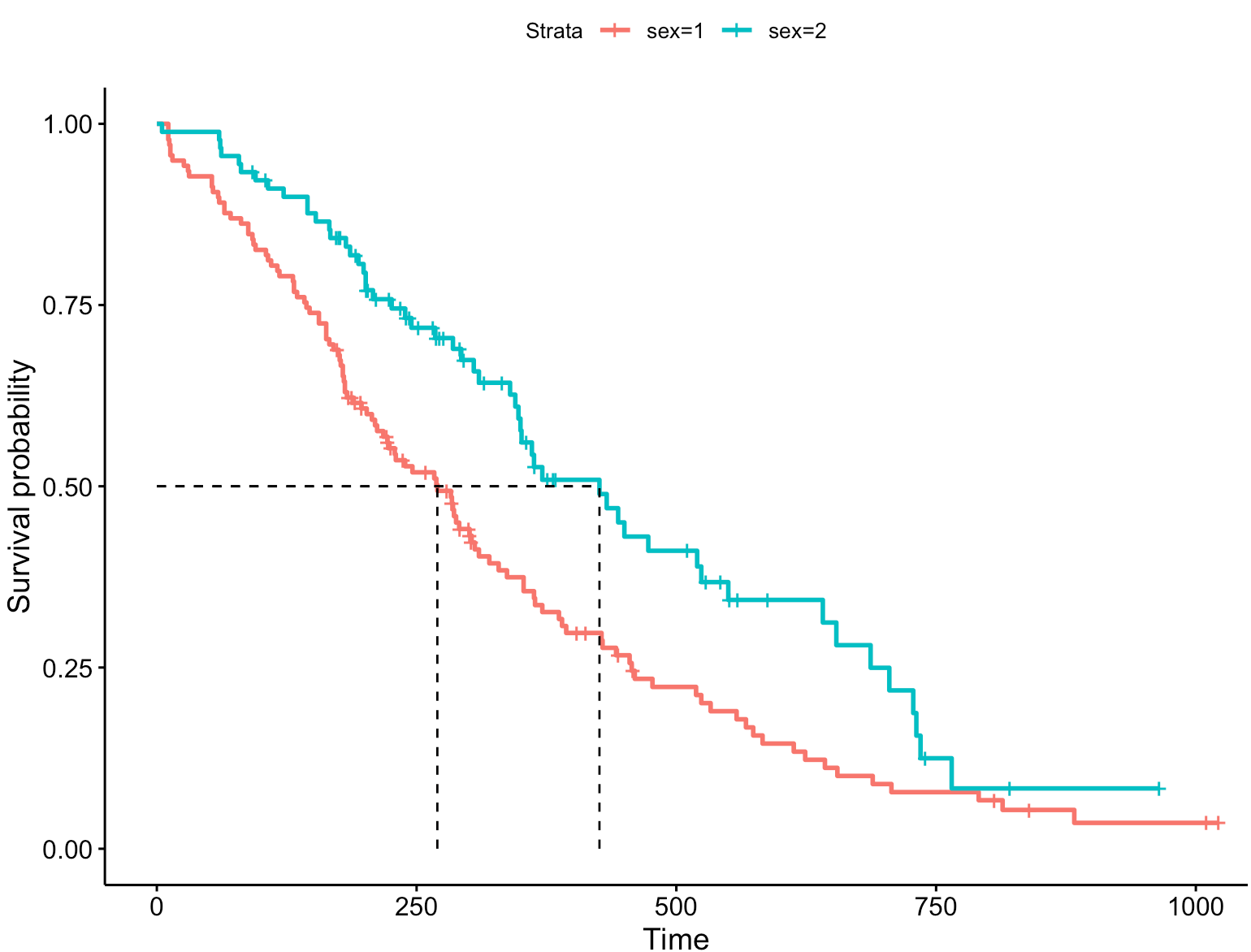
中位生存时间(median survival time)又称为生存时间的中位数，表示刚好有50%的个体其存活期大于该时间，是生存分析中常用的概括性统计量。

图解法是计算中位生存时间的方法。其利用生存曲线图，从纵轴生存率为50%处画一条与横轴平行的线，并与生存曲线相交，然后自交点画垂线与横轴相交，此交点对应的时间即为中位生存时间。

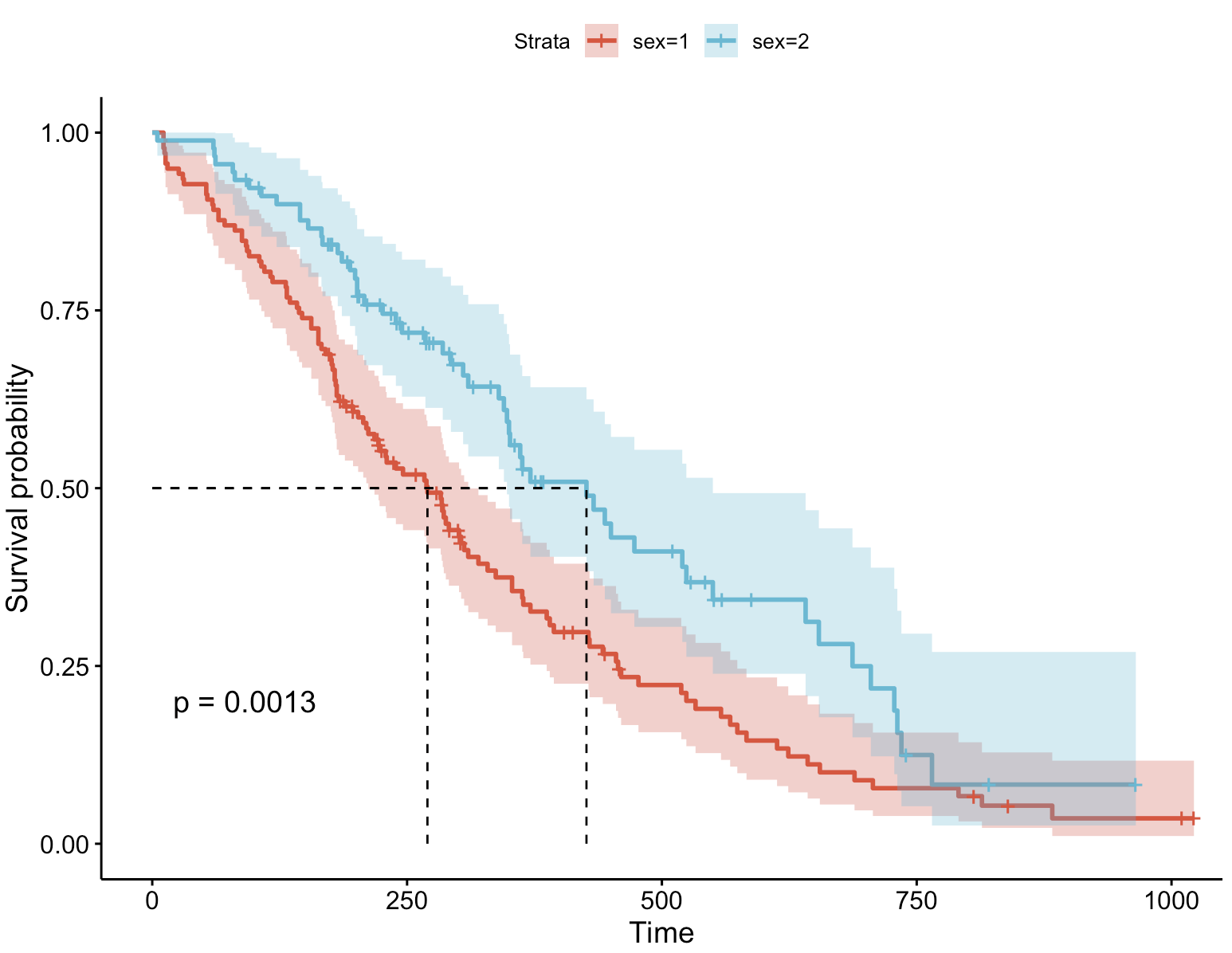
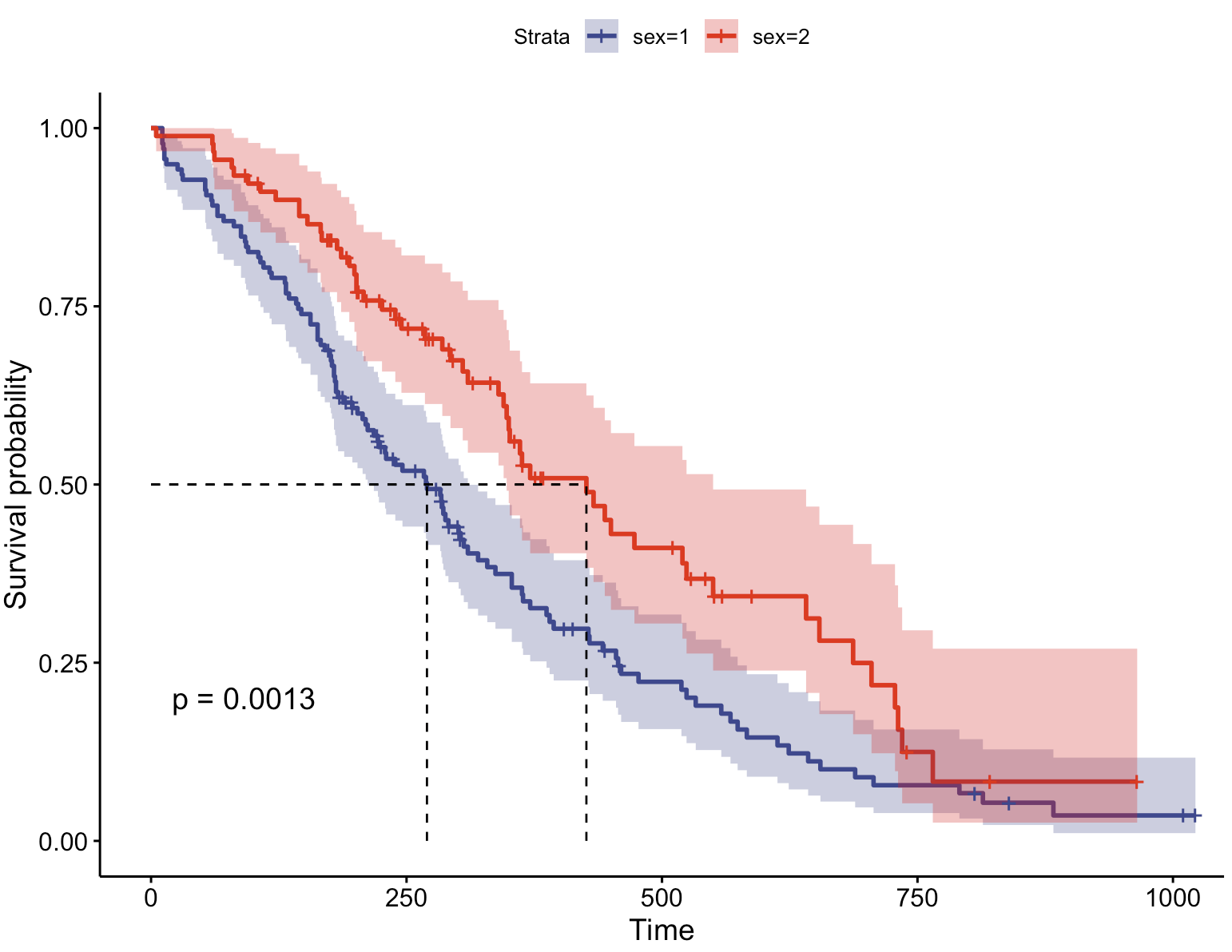
ggsurvplot(fit, data = lung, surv.median.line = "hv") # 增加中位生存时间

ggsurvplot(fit, data = lung, surv.median.line = "hv")：这行代码调用了 ggsurvplot() 函数来创建一个带有中位生存时间线的生存曲线图。
- fit：这是之前使用 survfit() 函数拟合的生存曲线对象。这个对象包含了生存数据的拟合信息，ggsurvplot() 将使用这些信息来绘制曲线。
- data = lung：这里指定了原始的生存数据集，ggsurvplot() 会用它来获取额外的信息，如中位生存时间或用于分层的变量值。
- surv.median.line = "hv"：这是一个参数，用于在生存曲线图中添加中位生存时间的线。这里的 "hv" 参数指定了中位生存时间线的形式，"h" 代表水平线，"v" 代表垂直线，意味着在中位生存时间点，既有一条水平线也有一条垂直线，以便于在图中清晰地识别中位生存时间。
函数执行：当执行 ggsurvplot() 函数时，它会生成一个生存曲线的图形，其中包含了根据 fit 对象拟合的生存曲线，并且根据 data 数据集中的信息，展示不同性别或组别（如果 fit 对象是分层拟合的）的生存曲线。同时，由于指定了 surv.median.line = "hv"，图中还会展示每个组的中位生存时间，通过水平和垂直线在图中标识出来。
图形输出：ggsurvplot() 函数默认会直接在R会话的图形设备上绘制图形。如果没有指定其他图形设备，它会在当前R会话的活跃图形设备上绘制。

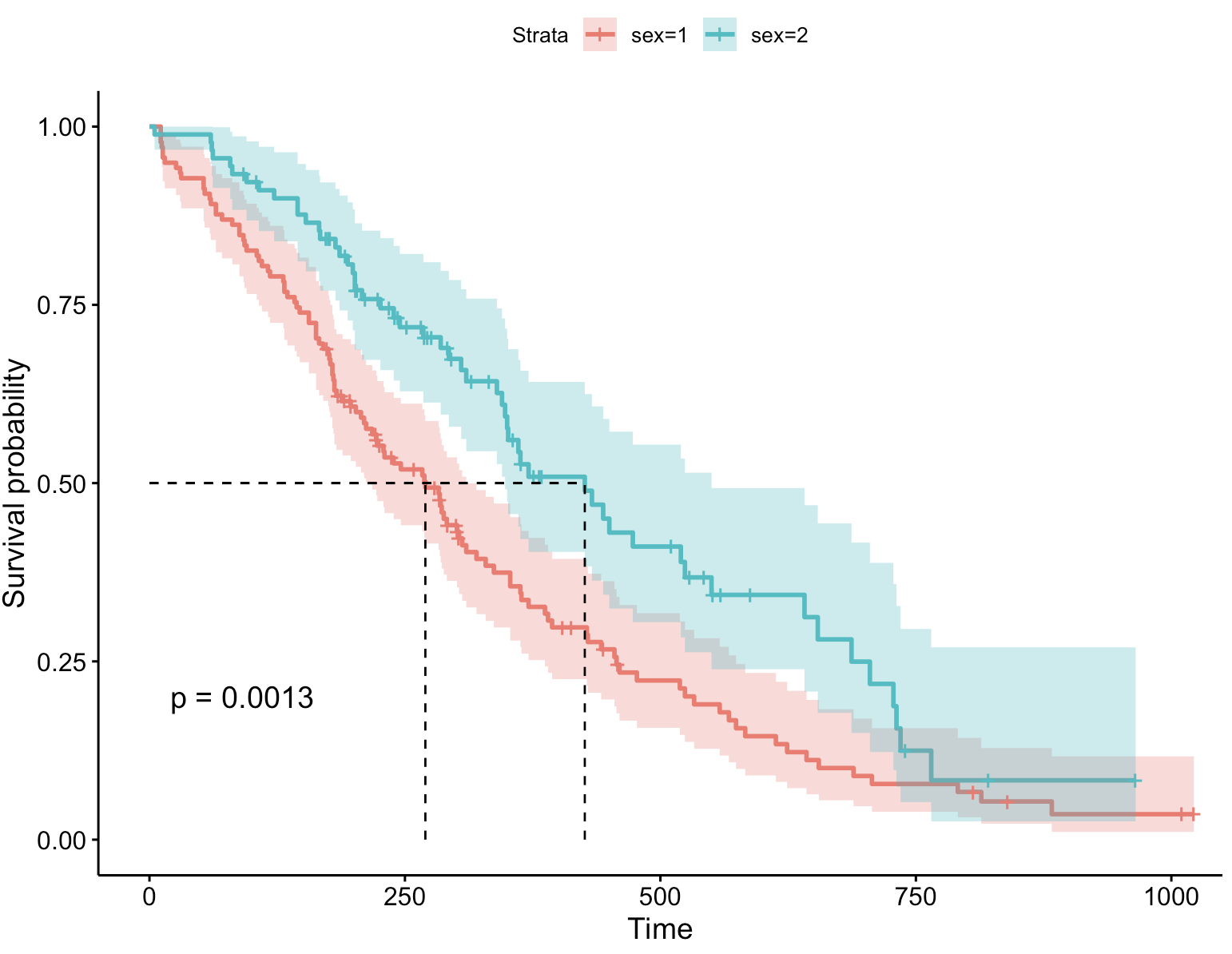
从图上可以看出，男性的中位生存时间小于女性。由之前的结果可知具体时间——男性为270，女性为426。

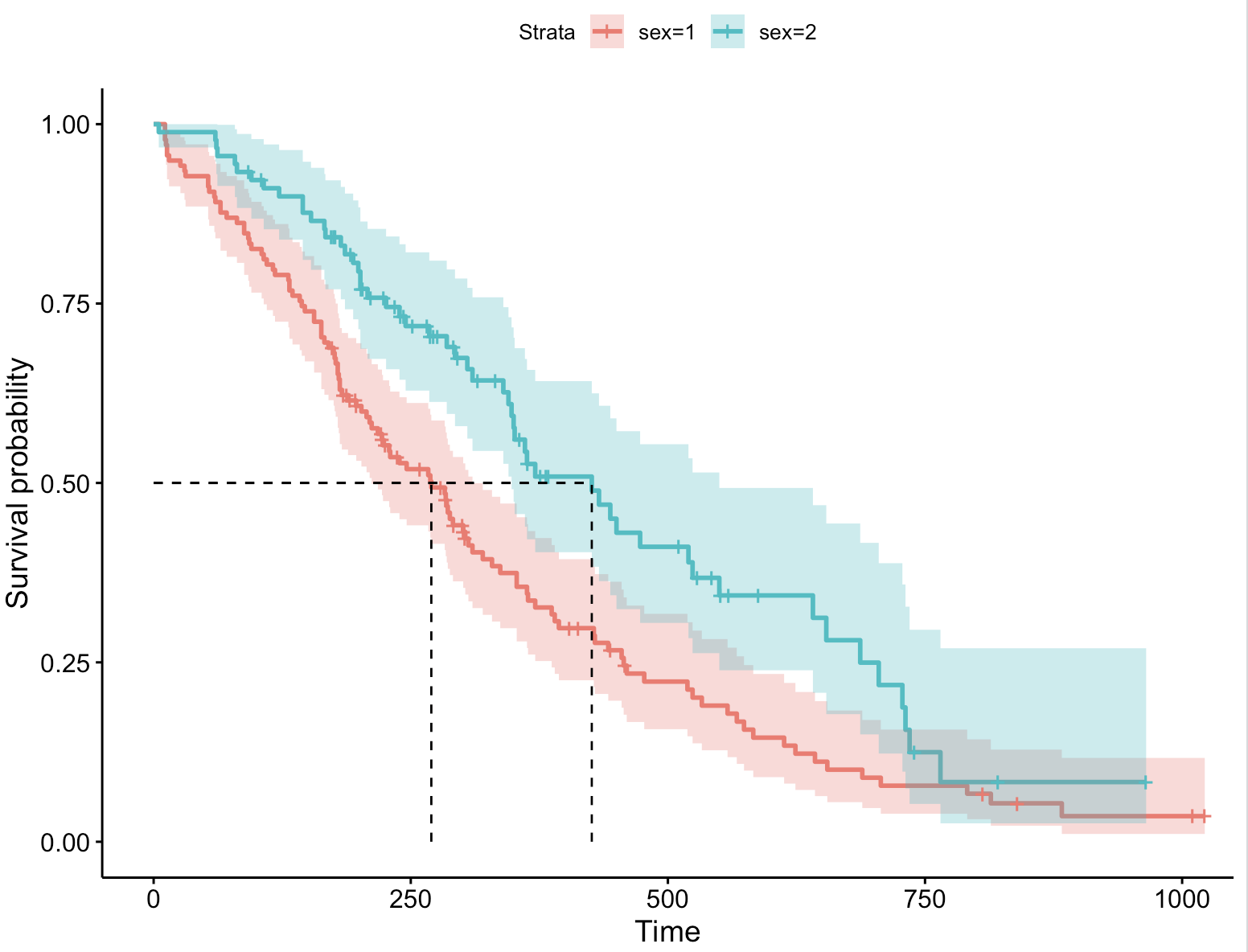
2、增加置信区间

ggsurvplot(fit, data = lung, surv.median.line = "hv",conf.int = TRUE) # 增加置信区间

conf.int = TRUE：这个参数设置了是否在生存曲线图中添加置信区间。设置为 TRUE 表示绘制生存曲线时，会包括对应的置信区间。

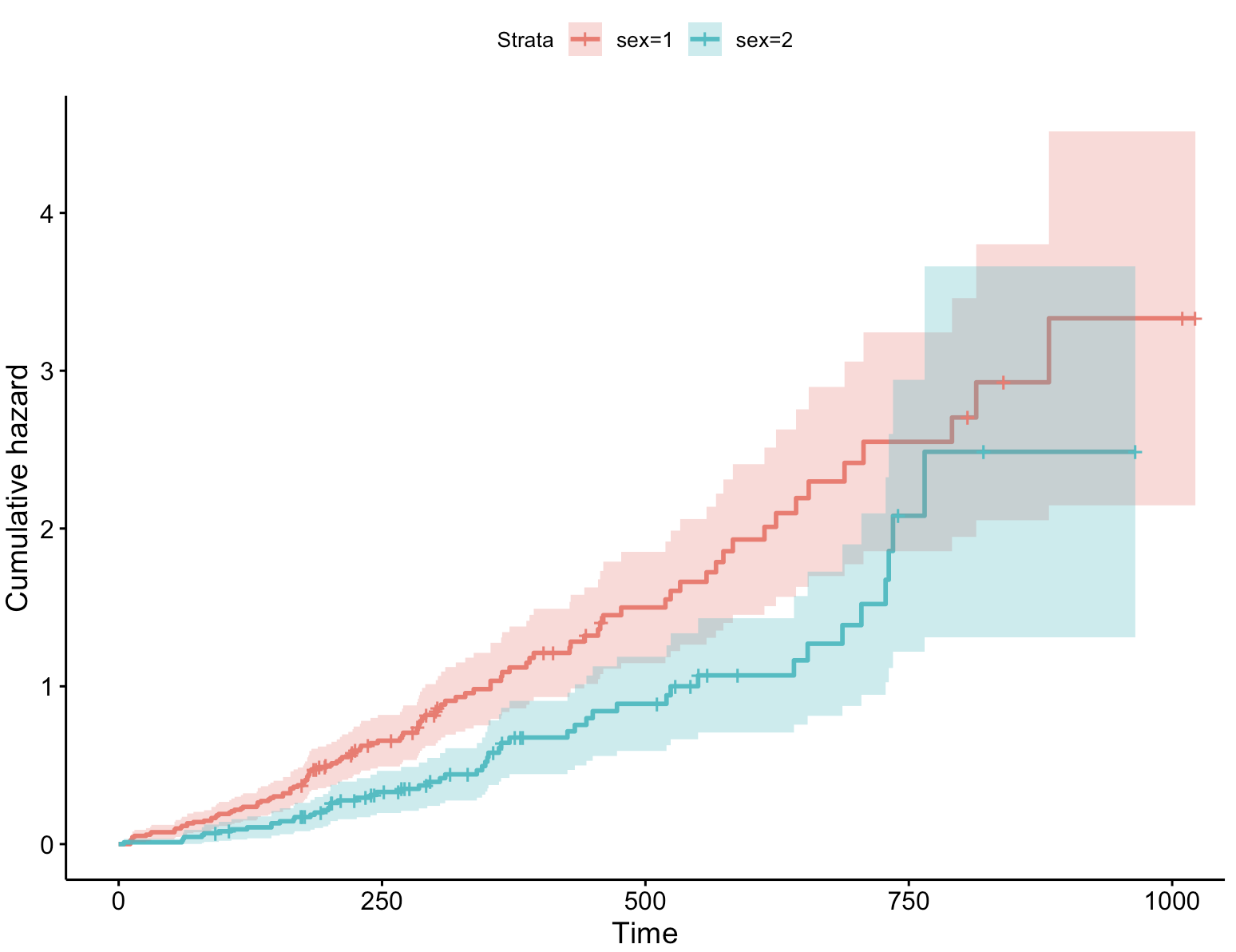
3、绘制累计风险曲线

在生存分析中，fun = "cumhaz" 是一个参数设置，通常用在 ggsurvplot() 函数中，用来指定绘制累积风险（cumulative hazard）曲线而不是默认的生存概率（survival probability）曲线。

下面是对 fun = "cumhaz" 的详细解释：

fun：这是一个参数，代表函数或者计算方法的选择。在 ggsurvplot() 函数中，fun 参数允许用户选择不同的计算和图形展示方式。
"cumhaz"：这是 fun 参数的一个选项，代表累积风险（Cumulative Hazard）。累积风险是一个衡量在特定时间或时间内之前发生事件的风险的指标。在生存分析中，累积风险是事件发生概率随时间累积的总和，可以用于描述生存数据中事件随时间发生的风险变化。

当你在 ggsurvplot() 函数中设置 fun = "cumhaz" 时，函数会生成累积风险曲线，而不是默认的生存曲线。累积风险曲线通常用于展示在不同时间点之前至少一次发生事件的累积概率。

ggsurvplot(fit, data = lung, conf.int = TRUE,fun = "cumhaz") # 绘制累计风险曲线

⚠️累积风险曲线在某些情况下比生存曲线更有用，尤其是在想要强调事件发生风险随时间的累积效应时。然而，累积风险曲线的解释可能比生存曲线更复杂，因此在选择使用时需要考虑分析的目的和受众。

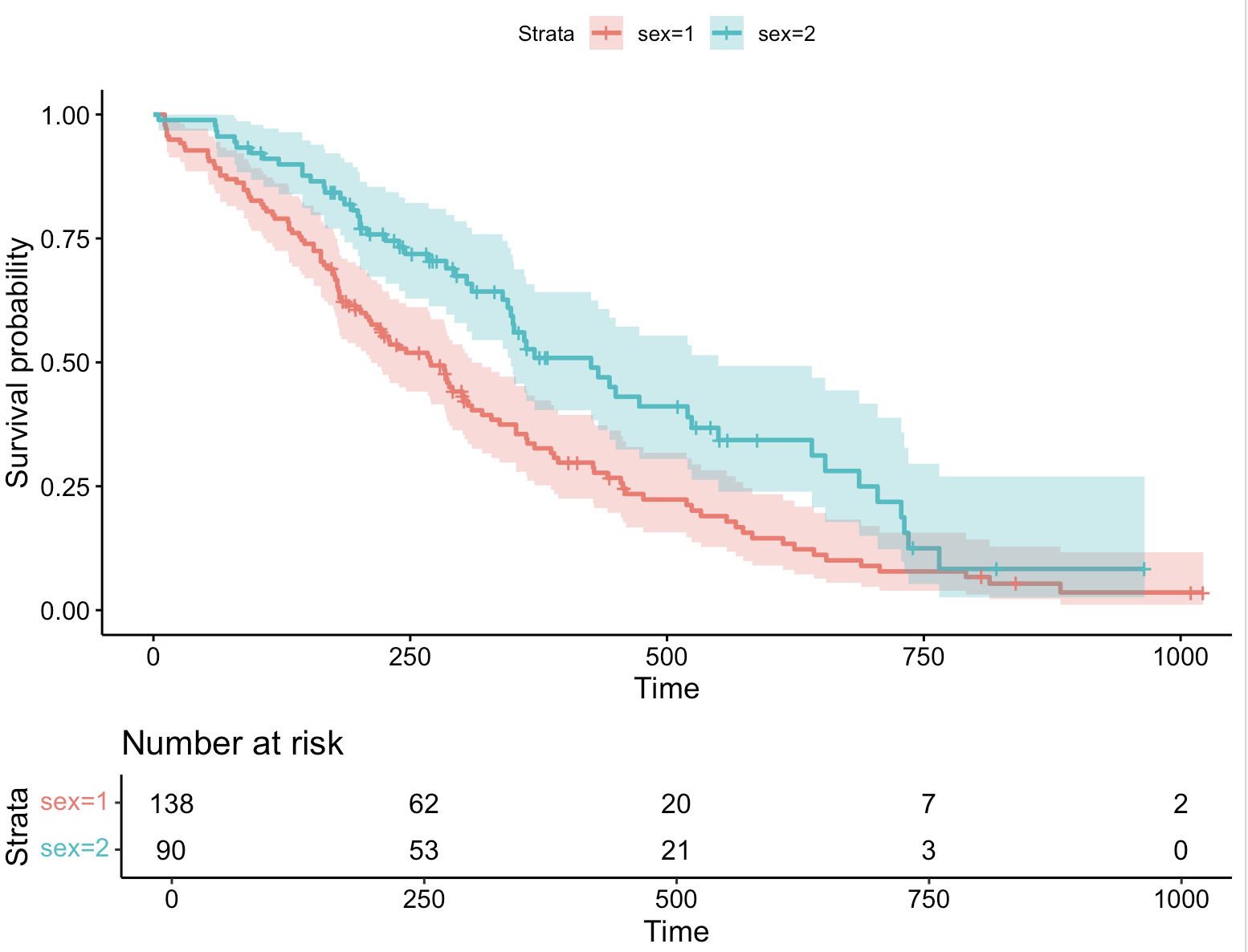
4、添加风险表

ggsurvplot(fit, data = lung, conf.int = TRUE,risk.table = TRUE) # 绘制累计风险曲线

5、添加总患者生存曲线

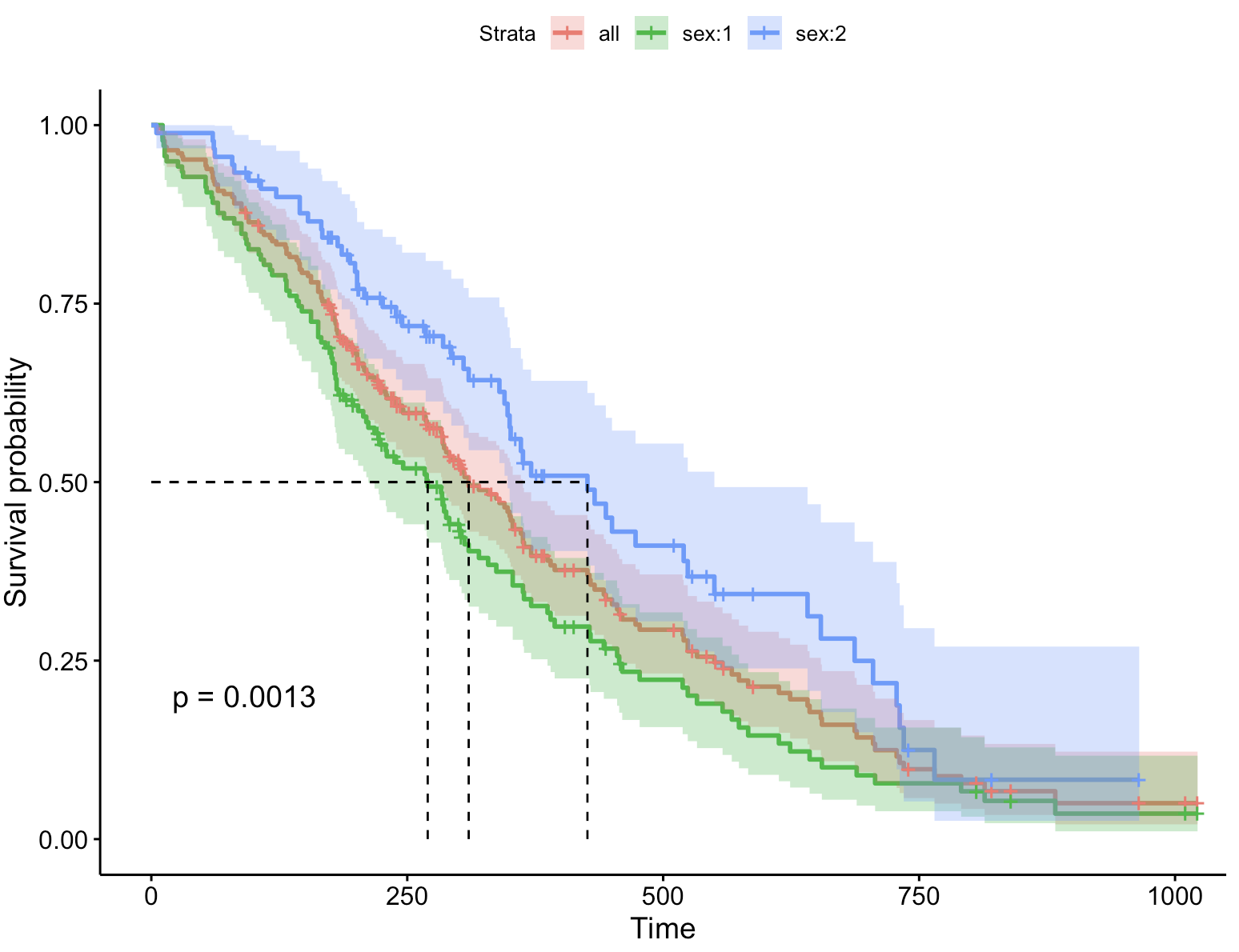
ggsurvplot(fit, # 创建的拟合对象  data = lung, # 指定变量数据来源  conf.int = TRUE, # 显示置信区间  pval = TRUE, # 添加P值  surv.median.line = "hv", # 添加中位生存时间线  add.all = TRUE) # 添加总患者生存曲线

6、自定义调色板

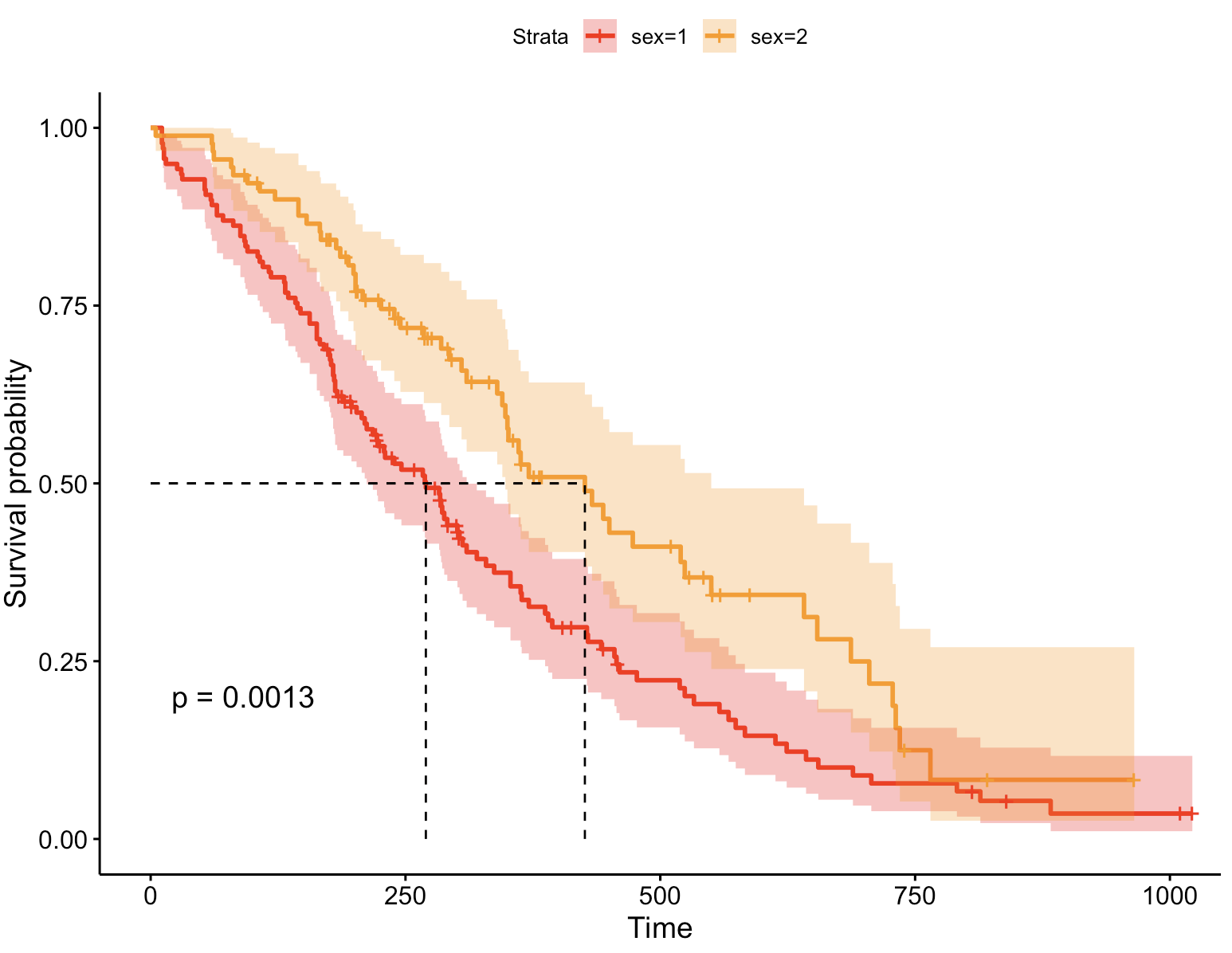
ggsurvplot(fit, # 创建的拟合对象  data = lung, # 指定变量数据来源  conf.int = TRUE, # 显示置信区间  pval = TRUE, # 添加P值  surv.median.line = "hv", # 添加中位生存时间线  palette = "hue") # 自定义调色板

可选调色板有 “grey”,“npg”,“aaas”,“lancet”,“jco”, “ucscgb”,“uchicago”,“simpsons”和”rickandmorty”.

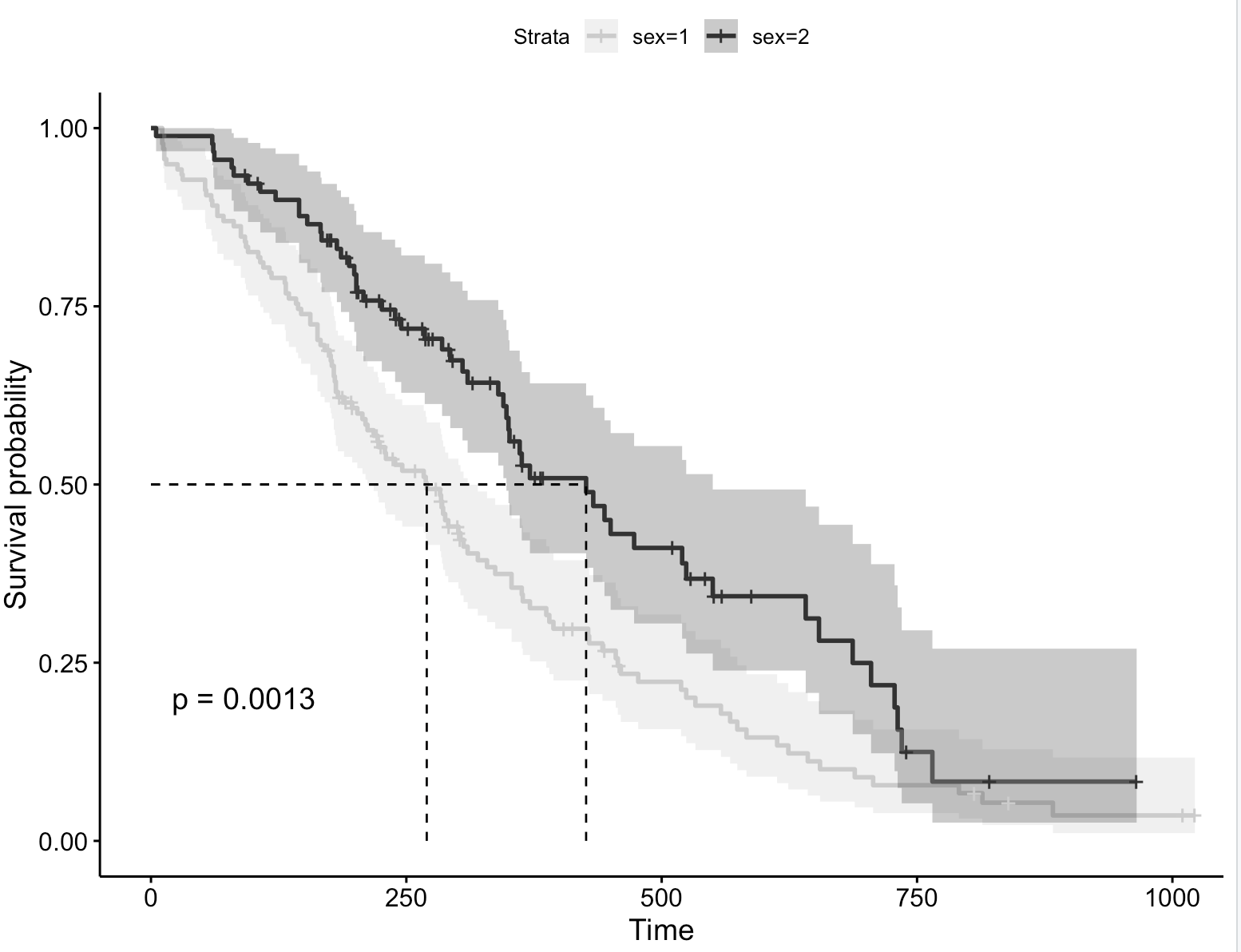
调色板：grey

ggsurvplot(fit, # 创建的拟合对象  data = lung, # 指定变量数据来源  conf.int = TRUE, # 显示置信区间  pval = TRUE, # 添加P值  surv.median.line = "hv", # 添加中位生存时间线  palette = "grey") # 自定义调色板

调色板：npg

ggsurvplot(fit, # 创建的拟合对象  data = lung, # 指定变量数据来源  conf.int = TRUE, # 显示置信区间  pval = TRUE, # 添加P值  surv.median.line = "hv", # 添加中位生存时间线  palette = "npg") # 自定义调色板

调色板：aaas

ggsurvplot(fit, # 创建的拟合对象  data = lung, # 指定变量数据来源  conf.int = TRUE, # 显示置信区间  pval = TRUE, # 添加P值  surv.median.line = "hv", # 添加中位生存时间线  palette = "aaas") # 自定义调色板

调色板：ucscgb

ggsurvplot(fit, # 创建的拟合对象  data = lung, # 指定变量数据来源  conf.int = TRUE, # 显示置信区间  pval = TRUE, # 添加P值  surv.median.line = "hv", # 添加中位生存时间线  palette = "ucscgb") # 自定义调色板

7、美化生存曲线

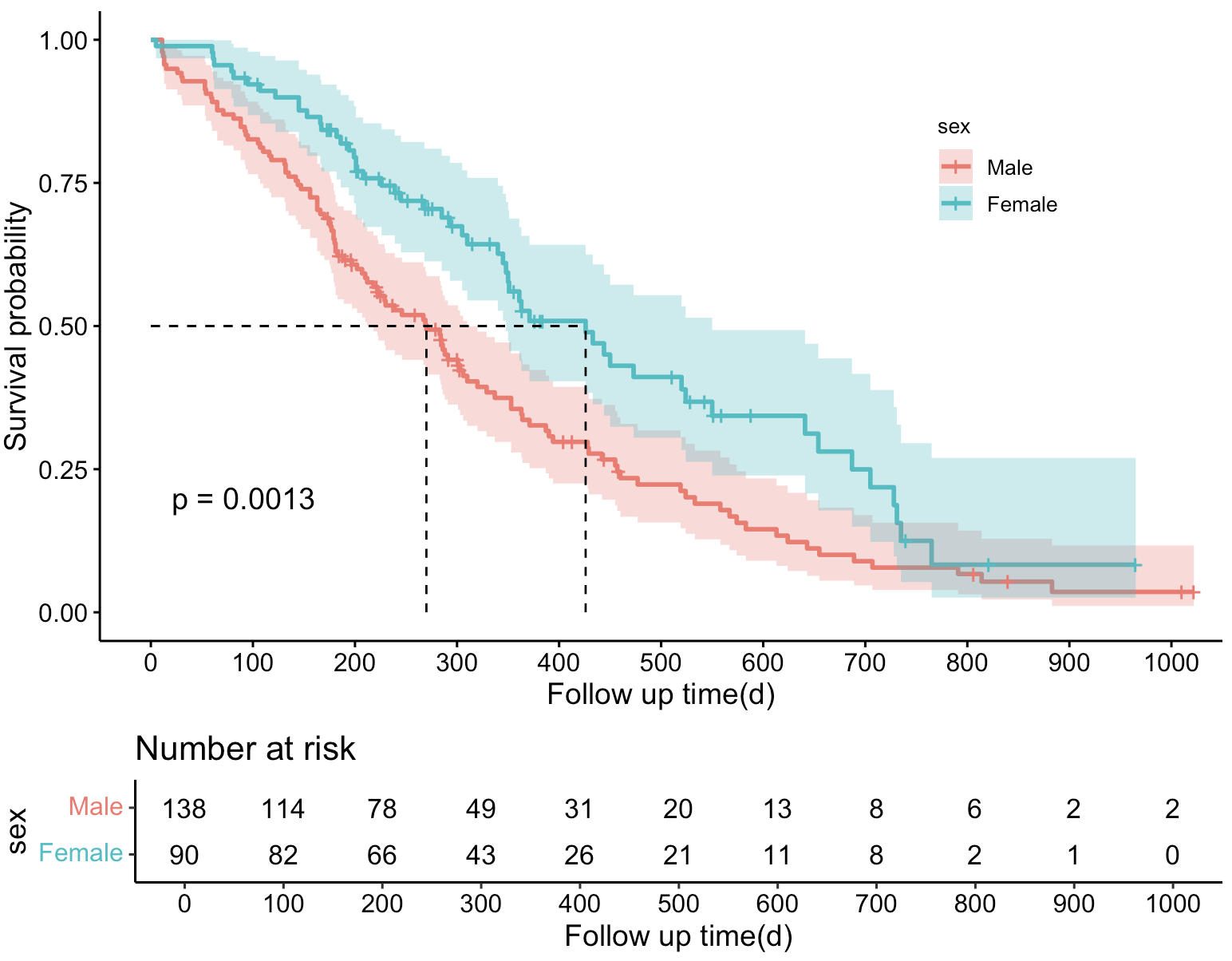
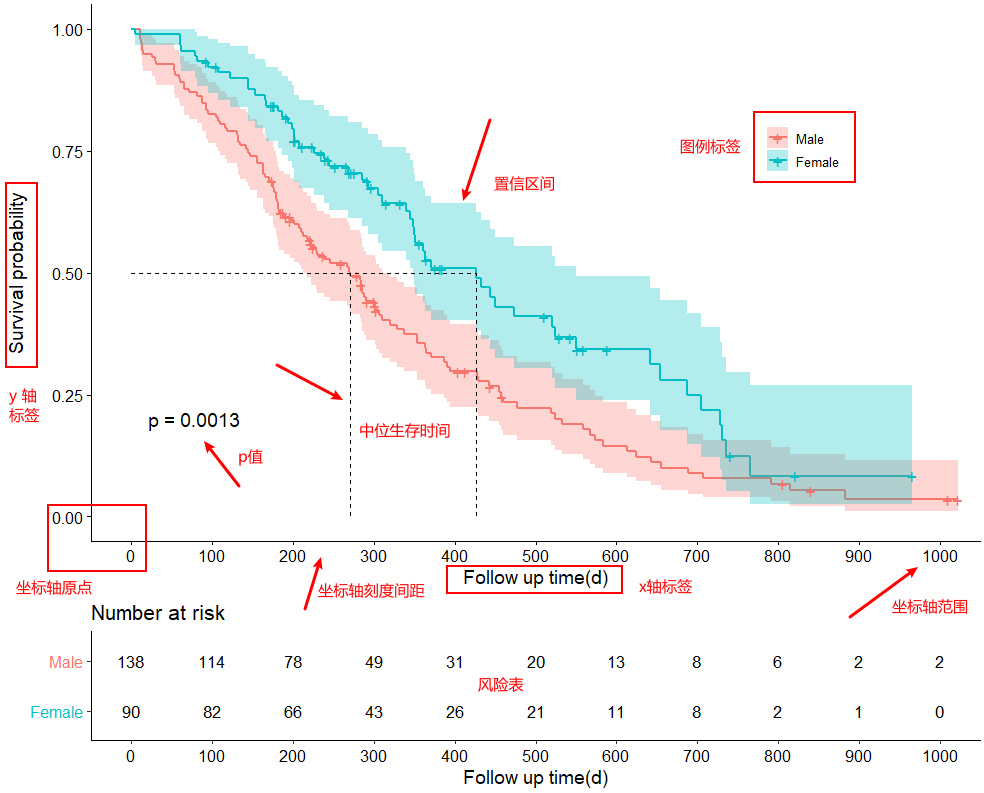
ggsurvplot(fit, # 创建的拟合对象  data = lung, # 指定变量数据来源  conf.int = TRUE, # 显示置信区间  pval = TRUE, # 添加P值  surv.median.line = "hv", # 添加中位生存时间线  risk.table = TRUE, # 添加风险表  xlab = "Follow up time(d)", # 指定x轴标签  legend = c(0.8,0.75), # 指定图例位置  legend.title = "sex", # 设置图例标题  legend.labs = c("Male", "Female"), # 指定图例分组标签  break.x.by = 100) # 设置x轴刻度间距

4-6： ggsurvplot()函数

1、主要参数

ggsurvplot(fit, data = NULL, fun = NULL, color = NULL, palette = NULL, linetype = 1, conf.int = FALSE, pval = FALSE, pval.method = FALSE, test.for.trend = FALSE, surv.median.line = "none", risk.table = FALSE, cumevents = FALSE, cumcensor = FALSE, tables.height = 0.25, group.by = NULL, facet.by = NULL, add.all = FALSE, combine = FALSE, ggtheme = theme_survminer(), tables.theme = ggtheme, ...)

fit # 拟合的生存曲线对象 data # 用来拟合生存曲线的数据集 fun # 常用三个字符参数； # "event"绘制累积事件(f(y)=1-y)， # "cumhaz"绘制累积危害函数(f(y)=-log(y)); # "pct"绘制生存概率(百分比)。 color # 设置生存曲线的颜色。 # 如果只有1条曲线，则直接设置color="blue"； # 如果有多条曲线，默认color="strata"，按分组为生存曲线着色； # 也可以自定义调色板来设置曲线颜色。 palette # 调色板，默认"hue"。 # 可选调色板有"grey","npg","aaas","lancet",  # "jco", "ucscgb","uchicago","simpsons"和"rickandmorty". linetype = 1 # 设置曲线线型。可以按"strata"设置线型； # 或按数字向量c(1, 2)或按字符向量c("solid", "dashed")设置 conf.int # 逻辑词；默认FASLE；为TRUE则绘制曲线置信区间 pval = FALSE # 逻辑词；为TRUE则将统计检验计算的p值添加到图上； # 为数字，则直接指定P值大小，如pval = 0.03； # 为字符串，则添加字符串到图上，如pval = "p-value: 0.031" pval.method # 逻辑词，是否添加计算p值的统计方法的文本； # 只有当 pval = TRUE时, 才会在图上添加检验方法文本 test.for.trend # 逻辑词，默认为FALSE； # 为TRUE则返回趋势p值的检验，趋势检验旨在检验生存曲线的有序差异 surv.median.line # 在中位生存时间点处绘制水平或垂直线的字符向量； # 可用值有"none"、"hv"、"h"、"v"；其中v绘制垂直线，h绘制水平线。 risk.table = FALSE # 逻辑词，图上是否添加风险表； # "absolute" 显示处于风险中的绝对数量； # "percentage" 显示处于风险中的百分比数量 # "abs_pct" 显示处于风险中的绝对数量和百分比 cumevents # 逻辑词，是否添加累计事件表 cumcensor # 逻辑词，是否添加累计删失表 tables.height = 0.25 # 生存曲线图下所有生存表的高度，数值0-1之间 group.by # 包含分组变量名称的字符向量，向量长度≤2 facet.by # 字符向量，指定绘制分面生存曲线的分组变量(应≤2)的名称 ggtheme=theme_survminer() # 设置ggplot2主题，如theme_bw() tables.theme # 作用于生存表的ggplot2主题名称 # 有theme_survminer、theme_cleantable() add.all = FALSE # 逻辑词；是否添加总患者生存曲线到主生存图中

2、图标题和坐标轴标签

title # 图表标题  xlab, ylab # 分别指x轴和y轴标签

3、图例标题和位置

legend # 指定图例位置的字符向量："top"(默认),"bottom","left","right","none"等。 # legend="none" 表示移除图例； # 图例位置也可用数字向量c(x，y)指定，x和y的值应在0到1之间。 legend.title # 图例标题，如legend.title = "Sex"。 legend.labs # 指定图例标签的字符向量, 替换fit中strata的名称，顺序应与strata一致。 # 如 legend.labs = c("Male","Female")

4、坐标轴范围、刻度间距

break.time.by # 设定坐标轴刻度间距 break.x.by # 设定x轴刻度的间距，如break.x.by = 100 break.y.by # 设定y轴刻度的间距，如break.y.by = 0.2 surv.scale # 生存曲线的比例转换。允许的值为"default"或"percent"。 xlim, ylim # 指定x轴和y轴的范围，如xlim = c(0,30), ylim = c(0,1) axes.offset # 逻辑词，默认为TRUE。为FALSE，则生存曲线图的坐标轴从原点开始。

5、置信区间

以下只有在conf.int = TRUE时才生效

conf.int.fill # 设置置信区间填充的颜色 conf.int.style # 设置置信区间的类型，有"ribbon"(默认),"step"两种。 conf.int.alpha # 数值，指定置信区间填充颜色的透明度； # 数值在0-1之间，0为完全透明，1为不透明。

6、P值文本大小和位置

以下只有在pval = TRUE时才生效

pval.size # 指定p值文本大小的数字，默认为 5。 pval.coord # 长度为2的数字向量，指定p值位置x、y，如pval.coord=c(x,y)。 pval.method.size # 指定检验方法 log.rank 文本的大小 pval.method.coord # 指定检验方法 log.rank 文本的坐标 log.rank.weights # 计算log-rank检验p值的权重类型的名称。

7、删失点

censor # 逻辑词，默认为TRUE，在图上绘制删失点。 censor.shape # 数值或字符，用于指定删失点的形状；默认为"+"(3), 可选"|"(124)。 censor.size # 指定删失点形状的大小，默认为4.5。

8、生存表

所有生存表的常规参数。指定以下参数时，可应用于所有生存表（风险表、累积事件表和累积删失表）。

tables.col # 生存曲线图下所有表的颜色，默认为"black"； # 按strata显示则tables.col="strata". fontsize # 指定风险表和累积事件表的字体大小。 font.family # 指定文字字体的字符向量,如font.family="Courier New". tables.y.text # 逻辑词，默认显示生存表的y轴刻度标签；为FALSE则刻度标签被隐藏 tables.y.text.col # 逻辑词，默认FALSE；为TRUE，则表的y刻度标签将按strata着色。 tables.height # 指定所有生存表的高度，数值在0-1之间，默认为0.25.

9、风险表

risk.table.title # 风险表的标题 risk.table.pos # 指定风险表位置的字符向量； # 有两种，"out"在生存图外(默认)，"in"在生存图内。 risk.table.col risk.table.fontsize risk.table.y.text risk.table.y.text.col risk.table.height # 这五个和上面生存表的常规参数意义是一样的 # 但是只应用在风险表中。

10、累积事件表

cumevents.title # 累积事件表的标题 cumevents.col cumevents.y.text cumevents.y.text cumevents.height # 这四个和上面生存表的常规参数意义是一样的 # 但是只应用于累积事件表中。

11、累积删失表

cumcensor.title # 累积删失表的标题 cumcensor.col cumcensor.y.text cumcensor.y.text.col cumcensor.height # 这四个和上面生存表的常规参数意义是一样的 # 但是只应用于累积删失表中。

12、生存图高度

surv.plot.height # 生存图的高度，默认为0.75； # 当risk.table = FALSE时忽略

13、字体样式

font.title # 标题字体 font.subtitle # 副标题字体 font.caption font.x、font.y # x轴、y轴字体 font.tickslab # 刻度标签字体 font.legend # 图例字体 用长度为3的向量分别指定大小、类型、颜色。如： # font.main = c(16, "bold", "darkblue") # font.x = c(14, "italic", "red") # font.y = c(14, "bold.italic", "darkred") # font.tickslab = c(12, "plain", "darkgreen") # font.x = 14 则只改变字体的大小 # font.x = "bold" 则只改变字体类型

五、导入外部数据集

现在假设我们需要导入一个格式为Excel的临床数据，则需要用到readxl包。

install.packages("readxl") library(readxl)

data <- read_excel("/Users/luoxiaoluotongxue/Desktop/硕士课题进展记录/3月测试/test.xlsx")

现在我们来简单的查看一下数据。

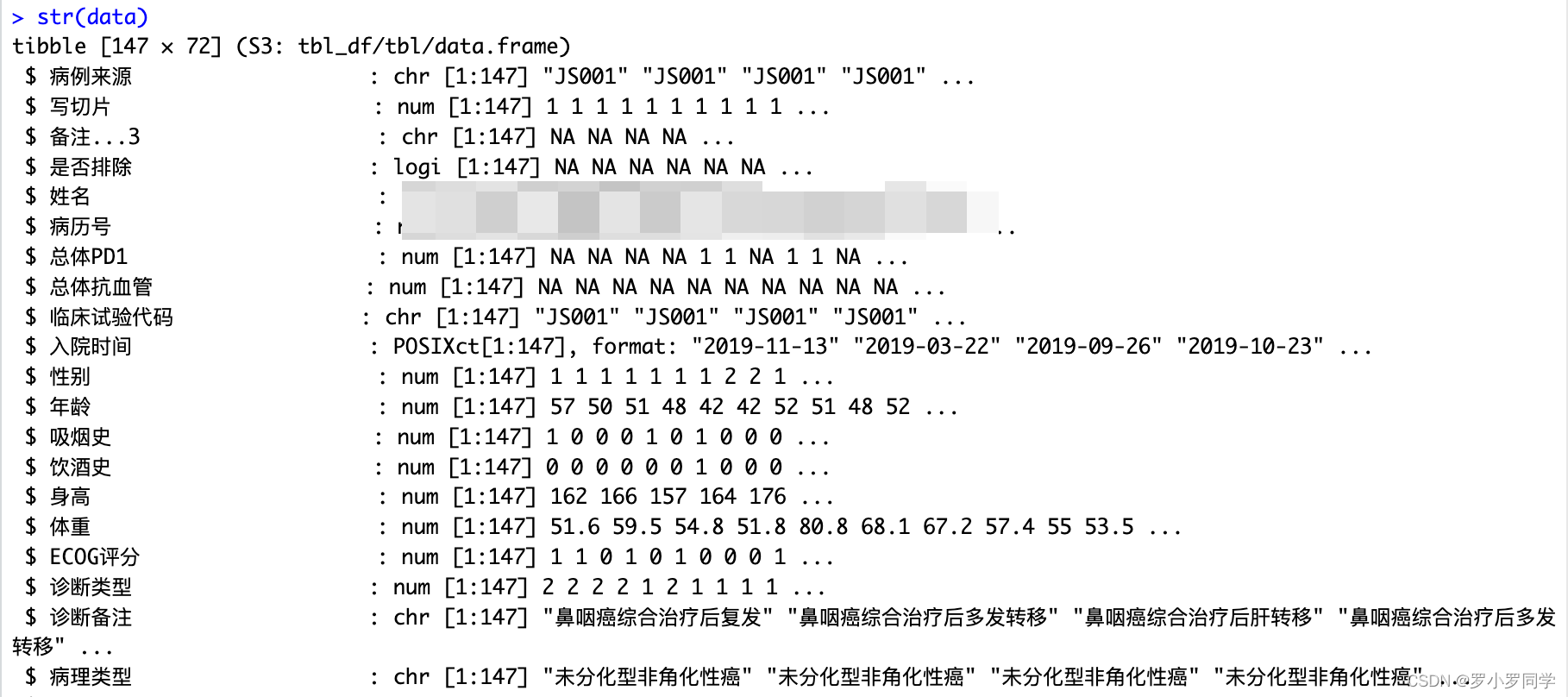
# 查看数据的前几行 head(data) # 查看数据的结构，包含列名和数据类型 str(data) # 查看数据的概要信息，包括每列的概要统计 summary(data) # 查看数据的行数和列数 dim(data)

查看数据的前几行

查看数据的结构，包含列名和数据类型

查看数据的概要信息，包括每列的概要统计

查看数据的行数和列数

现在我们开始往下走。

创建生存对象

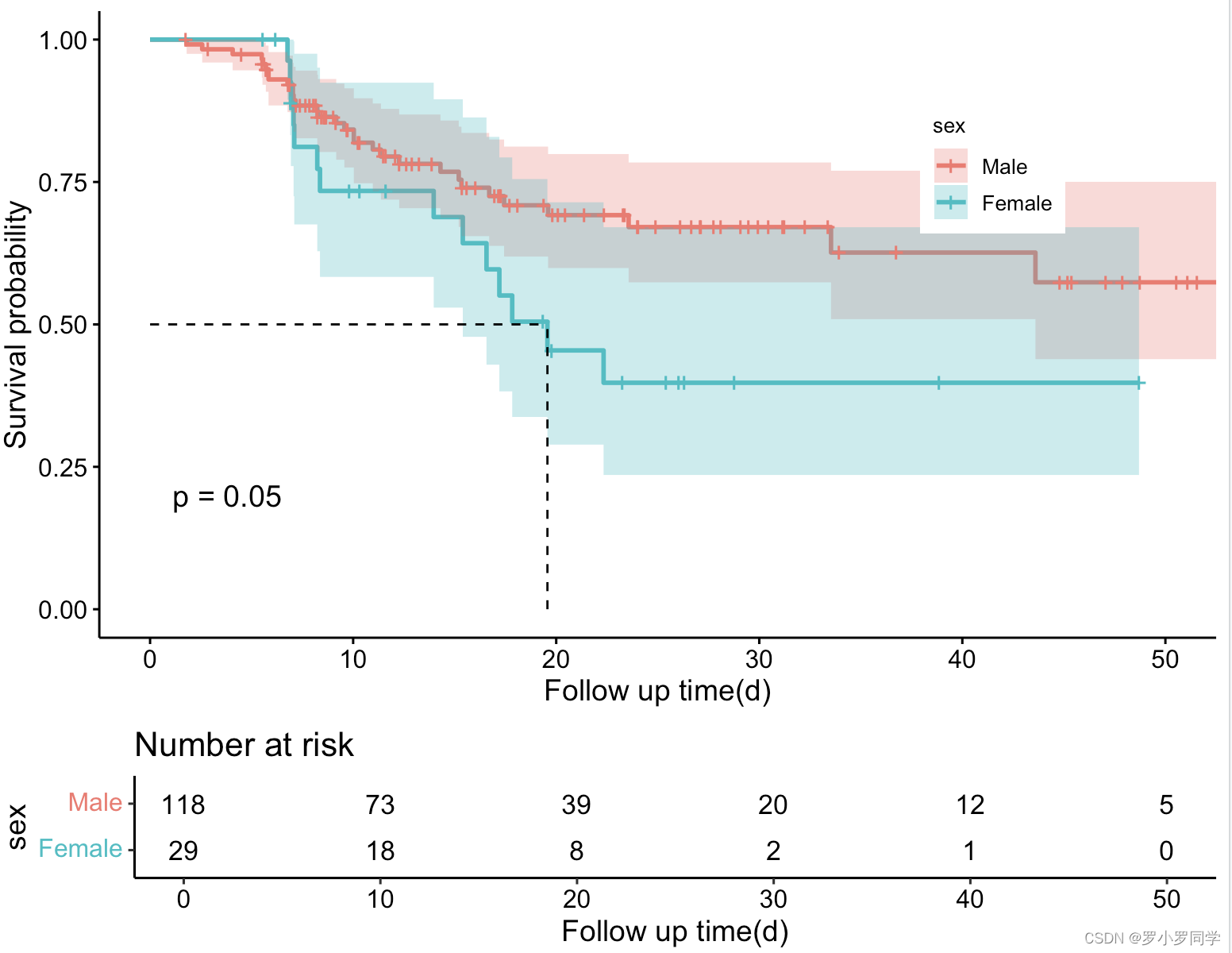
Surv(PFS,是否死亡) # 创建生存对象 fit <- survfit(Surv(PFS,是否死亡) ~ 性别,data = testData) # 数据集来源 fit

绘制生存曲线

ggsurvplot(fit, # 创建的拟合对象  data = testData, # 指定变量数据来源  conf.int = TRUE, # 显示置信区间  pval = TRUE, # 添加P值  surv.median.line = "hv", # 添加中位生存时间线  risk.table = TRUE, # 添加风险表  xlab = "Follow up time(d)", # 指定x轴标签  legend = c(0.8,0.75), # 指定图例位置  legend.title = "sex", # 设置图例标题  legend.labs = c("Male", "Female"), # 指定图例分组标签  break.x.by = 10) # 设置x轴刻度间距

免责声明：本站所有文章内容,图片，视频等均是来源于用户投稿和互联网及文摘转载整编而成，不代表本站观点，不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益，请在线联系站长,一经查实,本站将立刻删除。本文来自网络,若有侵权，请联系删除，如若转载，请注明出处：https://haidsoft.com/132349.html