十进制与二进制之间转换详解

大家好，欢迎来到IT知识分享网。

十进制与二进制之间转换详解

（一）十进制数转二进制数

1.1 十进制正整数转二进制

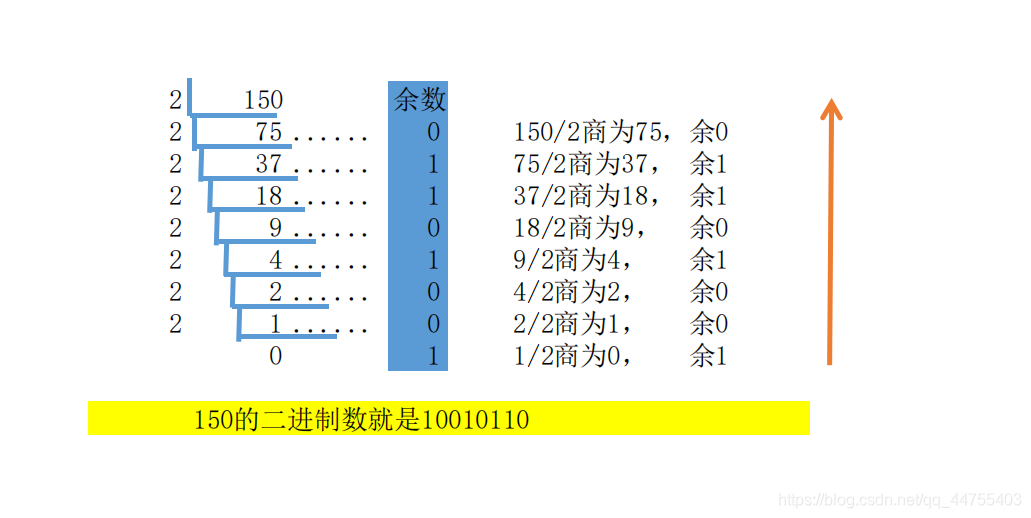
【基本原理】：除基数倒取余数法。
即：十进制转二进制，基数就是2，用2整除一个十进制正整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数；如此进行，直到商为0；然后把先得到的余数作为二进制数的低位有效位，把后得到的余数作为二级制的高位有效位，依次排列起来。所谓有效位，就是不算前导0；

 注：计算机内部表示数的字节单位是定长的，如8位，16位，32位。所以，位数不够时，高位补0， 

例如：输入十进制正整数：150

150

#include<iostream> using namespace std; int main() { 
    int i, j;//定义循环变量； int a[1005];//定义一个储存二进制的数组； int num; cin >> num;//输入需要转换的10进制正整数； for (i = 0; num != 0; i++) { 
    a[i] = num % 2;//对num取余.......就是除以2的余数； num = num / 2;//......每次取余之后num除以2的商； } for (j = i - 1; j >= 0; j--)//倒序输出余数，即为二进制数； { 
    cout << a[j]; } cout << "\n"; return 0; } 

for (j = i – 1; j >= 0; j–)
这里解释一下这句为什么是 (j=i-1),例如输入150，执行完循环之后 i=8;,但a数组的最后一个元素的下标是7（数组下标从0开始），所以i要减一；

1.2 十进制负整数转二进制

【方法】：先将十进制负整数对应的十进制正整数转换成二进制后，对二进制逐位取反（即：0变成1，
1变成0），然后对结果加1（当然是二进制运算）；

1.3 十进制小数转二进制数

0.125

注：如果十进制小数的整数部分有大于0的数时，将整数部分转成二进制，小数部分也转成二进制，加在一起就好了。
例：

150.125

（二） 二进制数转成十进制数

2.1 二进制整数转十进制

【基本原理】：按权展开求和法。
【方法】：首先将二进制数补齐位数（8位），首位如果是0就代表是正整数，如果首位是1则代表是负整
数。
（1）.补齐位数以后，若首位是0的正整数，将二进制中的各位数与各自的权相乘，然后求和。
例：

11010

（2）.补齐位数以后，若首位是1的负整数，就先将其逐位取反，再将二进制中的各位数与各自的权相乘，然后求和。
例：

2.1 二进制小数转十进制

0.1101

（三）十进制正整数转八进制

【基本原理】：与十进制正整数转二进制一样，除基数倒取余数法。
直接看代码：

#include<iostream> using namespace std; int main() { 
    int i, j;//定义循环变量； int a[1005];//定义一个储存八进制的数组； int num; cin >> num;//输入需要转换的10进制整数； for (i = 0; num != 0; i++) { 
    a[i] = num % 8;//对num取余.......就是除以8的余数； num = num / 8;//......每次取余之后num除以8的商； } for (j = i - 1; j >= 0; j--)//倒序输出余数，即为八进制数； { 
    cout << a[j]; } cout << "\n"; return 0; } 

150