大家好,欢迎来到IT知识分享网。
什么是自动控制原理?它是一种方法论,是通过传感器采取系统现在的状态,然后进行比较计算,然后通过控制器对系统进行调节,使其达到目标。
这个方法论应用广泛,比如在工业、军事、船舶、运输等方面。总的来说,自动控制原理给各个领域带来了许多优势,比如提高生产效率、降低能源消耗、提高系统的准确性。
接下来就是我将说明我所理解的自动控制原理:
目录
绪论
先了解自动控制原理的时候,我认为应该先进行一个铺垫:
上述已经表明自动控制原理是什么,其最重要的是在没有人的参与下完成我们设置的既定目标。在这种思想的指引下,我们通过控制各项机器来造福人类社会。
根据上述对于自动控制原理的描述,我们可以利用示意图的形式描述它:
从上述图像可以看出一个自动控制系统的最基础的结构是怎样的, 硬件方面要有控制器、被控的对象和一个检测元件,它们不同的作用共同撑起了一个简单的自动控制系统。首先控制器得到了我们想要实现想要的结果所输入的一个数据,经过控制器的计算得出数据输出给受控对象(或者执行器)做出我们想要的结果,这里我们通过检测元件(或者传感器)收集受控对象的数据输出到控制器与我们的给定值是否一致,如果不一致,系统就会通过控制器不断调整,反之保持。
可是我们怎样设计一个自动控制系统呢?还有就是现有一个现成的自动控制系统,我们怎样分析它呢?它的性能是怎样的?如果我要组装一个设备,将它放在里面合不合适?这些都是我们接下来要讨论的问题。
要想研究一个自动控制系统最好的办法是转换成我们能够看懂的语言–数学,数学是我们研究事物道理的工具,它帮助我们理解世界。数学的语言是非常简洁的,是逻辑鲜明的,能更好的描述自动控制系统,使我们更好的设计或者理解系统。
那我们利用数学的那一部分来研究呢?那么我们先从时域和频域对自动控制系统进行分析,这就需要我们对系统进行抽象建模,并利用傅里叶变换和拉普拉斯变换进行模型分析。接下来我们应该对于系统建模进行说明。
系统建模
系统方框图
我们怎么理解这个系统呢?举一个简单的系统:水温人工控制系统
如图所示:
从图中可以看出我们可以看到要想得到热水,就需要将蒸汽通过手动调节阀到达水箱,通过冷水进行降温输出热水,但是我们可以发现你想得到合适的热水,你只能通过调节调节阀改变蒸汽流量,来控制热水的温度,这就需要我们通过感觉和经验来调节,这样很难实现高质量的控制。
对于上面这种有人参与就不能称之为自动控制系统,那么我们怎样更改才能变成呢?我们根据自动控制原理的描述找到了答案,不能有人,那用什么呢?我们很快就能得到答案–机器。那我们可以将上述系统更改为以下系统:
从图中可以看出利用测温元件代替了我们的感觉和经验,执行机构代替了我们的手,实现了热水的温度控制。这就能很好的实现输出我们想要的适合的温度热水,不用在利用人来控制热水。
从上面我们可以看到控制器、执行器和被控对象,但是上图并不直观,有很多的输入,这样很容易混淆,于是我们找出被控量的通路形成一个流程图来更直观的控制。
系统方框图用来表示系统各个部件及变量之间的关系:
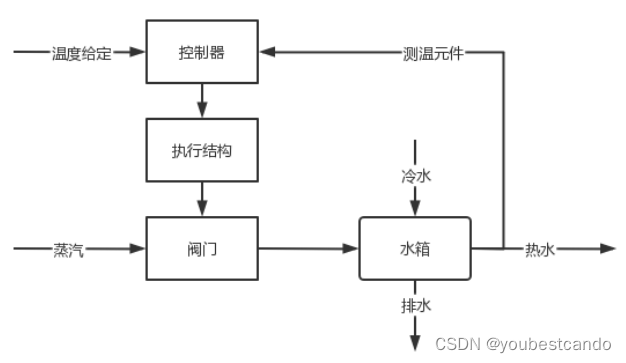
更改后的水温控制系统的系统框图:
这就完成了对于一个自动控制系统的模型建立,这个系统框图能够帮助人们理解系统的结构和功能,并且能够分析系统的各项指标等等。
系统控制方式、分类和性能要求
根据更改后的水温控制系统可知,有反馈,那么可知还有其他的情况,不然在其他情况下这种控制方式可能不适合。
那么有哪些控制方式呢?
一是开环控制,二是闭环控制,三是复合控制,其中复合控制有两种情况:一是按输入前馈补偿的复合控制;二是按扰动前馈补偿的复合控制。
系统分类:
线性系统和非线性系统;定常系统和时变系统;连续系统和离散系统;恒值系统、随动系统和程序控制系统。
系统的控制要求(三要求):稳定性、快速性、准确性。
了解完了自动控制系统的定义,控制方式、系统方框图、分类等情况,我们基本上可以进入数学的领域了,对自动控制系统进行一个分析。
数学模型
对于自动控制系统要想研究就需要进行数学分析,这样才能很好的评估系统的优劣。
通常一个系统是由一些环节连接而成的,我们需要得出每一个环节的微分方程,然后联立消除中间变量,最后得出系统的微分方程。
那么求取方程的步骤是什么?
(1)确定系统的输入变量和输出变量。
(2)建立初始微分方程组。
(3)消除中间变量,得出标准方程。
举一个例子看看:
如图所示,一个RC电路
根据步骤可得:
(1)确定输入量和输出量
输入量:ur(t);输出量:uc(t)
(2)建立初始微分方程组
由基尔霍夫定律得:
ur(t)=Ri(t)+uc(t) i(t)=C(duc(t)/dt)
(3)消除中间变量,得出标准方程
RC(duc(t)/dt)+uc(t)=ur(t)
其他系统也是如此得出标准方程,无论多么复杂的系统,都能利用部分求整体的思想得到标准方程。在建立初始微分方程组的时候,要灵活运用相应的物理定律,实现方程组的建立。
接下来将对线性方程式做出求解:
例:
系统的微分方程为:
已知:
解:对于微分方程两边进行拉普拉斯变换,注意零初始条件:
注意
整理得出:
最后拉普拉斯反变换得:
总而言之,要想研究自动控制系统,需要对系统进行建模,并擅长使用数学和物理规则。
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/142002.html