DFS与BFS优先搜索算法

大家好，欢迎来到IT知识分享网。

1.什么是BFS与DFS

1.1 什么是BFS

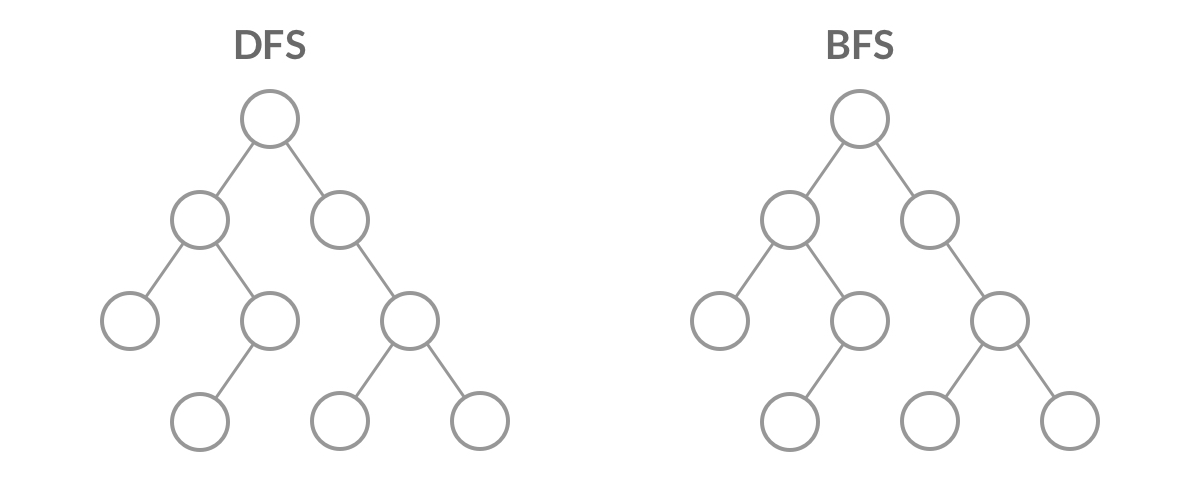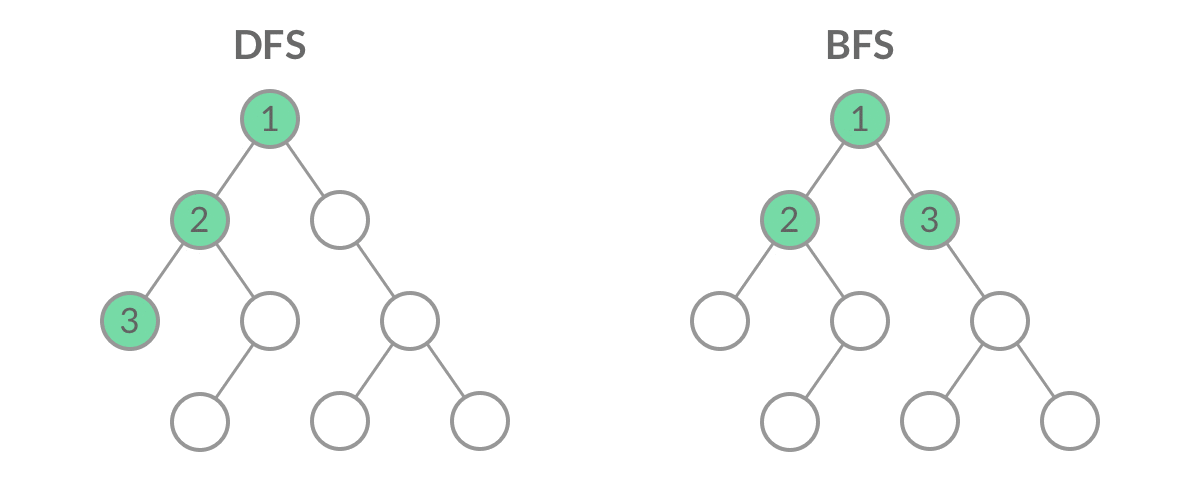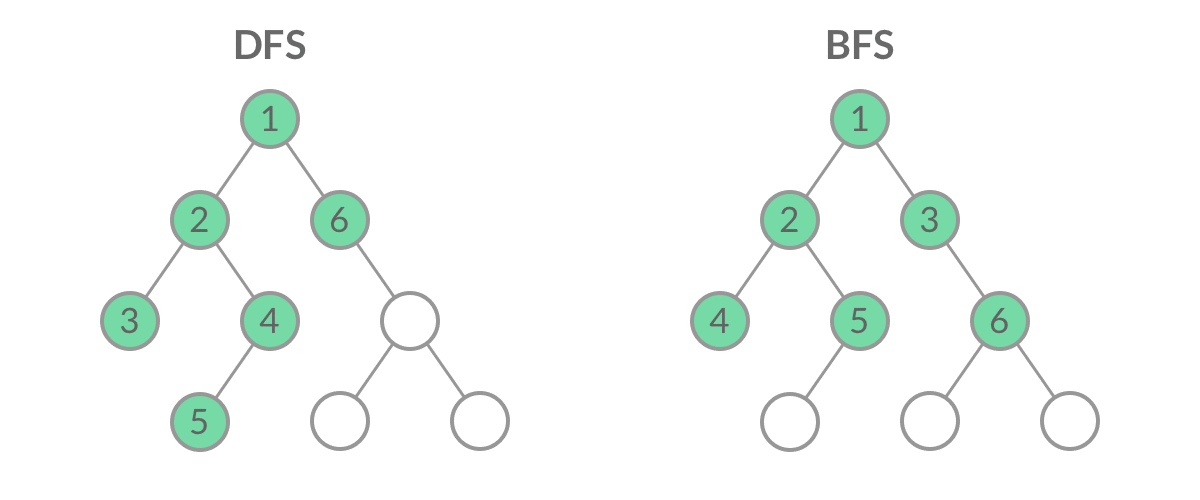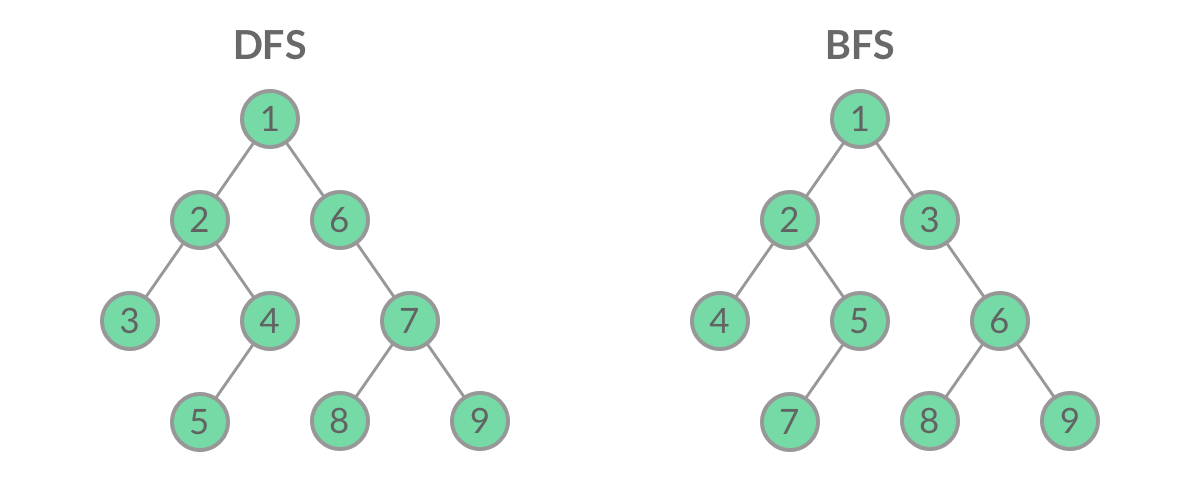
BFS（广度优先搜索）是一种图遍历算法，它从一个起始点开始，逐层扩展搜索范围，直到找到目标节点为止。

这种算法通常用于解决“最短路径”问题，比如在迷宫中找到从起点到终点的最短路径

        1.首先，你会从起点开始，检查所有与它相邻的位置，也就是距离起点为1的位置
        2.然后，你会继续向外扩展，检查所有距离起点为2的位置，以此类推，直到找到出口
在BFS中，你可以使用队列来存储待搜索的节点。起始点首先加入队列中，然后不断从队列中取出节点，检查它是否是目标节点。如果不是，就将它的所有未被访问过的邻居加入队列中。这样，队列中的节点总是按照它们距离起点的距离排序，先加入队列的节点总是先被取出来搜索。

通过这种方式，BFS可以找到起点到目标节点的最短路径。在实际应用中，BFS还可以用于拓扑排序、连通性检测等问题的解决。

1.2 什么是DFS

DFS（深度优先搜索）是一种图遍历算法，它从一个起始点开始，一直往下走直到不能再走为止，然后返回到前一个节点，继续探索它的其他分支，直到找到目标节点为止。这种算法通常用于解决“遍历”问题，比如在树中查找所有的叶子节点。

要理解DFS，也还可以想象自己在迷宫中寻找所有可行的路径

        1.首先，你会从起点开始，顺着一条路一直走，直到你走到一个死胡同
        2.再返回到前一个节点，继续探索其他分支
在探索过程中，你可以使用栈来存储已经访问过的节点，以便后续回溯。

在DFS中，你可以使用递归或栈来实现深度优先搜索。通过这种方式，DFS可以找到所有可行的路径，或者在树中查找所有的叶子节点。

在实际应用中，DFS还可以用于拓扑排序、连通性检测等问题的解决。与BFS相比，DFS通常更适合处理深度优先的问题，而BFS更适合处理广度优先的问题。

接下来，让我们先看看在二叉树上进行 BFS 遍历和 DFS 遍历的代码比较

首先是DFS 遍历使用递归(递归的方式隐含地使用了系统的栈)：

void dfs(TreeNode* root)  {     if (root == nullptr)      {         return;     }     // 依次递归遍历它的左子树和右子树     dfs(root->left);     dfs(root->right); } 

其次，BFS 遍历使用队列数据结构：

void bfs(TreeNode* root)  {     // 创建一个队列     queue<TreeNode*> q;     q.push(root);     while (!q.empty())      {         // 在每次循环中，使用 q.front() 获取队头节点，并将其出队         TreeNode* node = q.front();         q.pop();           // 检查这个节点的左右子节点是否为空，如果不为空，就将它们加入队列中         if (node->left != nullptr)          {             q.push(node->left);         }         if (node->right != nullptr)         {             q.push(node->right);         }     } }

2.应用BFS求解的典型问题：层序遍历

例题：二叉树的层序遍历

给定一个二叉树，返回其按层序遍历得到的节点值。 层序遍历即逐层地、从左到右访问所有结点。

什么是层序遍历呢？简单来说，层序遍历就是把二叉树分层，然后每一层从左到右遍历 

乍一看，这个遍历顺序和 BFS 是一样的，我们可以直接用 BFS 得出层序遍历结果。然而，层序遍历要求的输入结果和 BFS 是不同的。层序遍历要求我们区分每一层，也就是返回一个二维数组。而 BFS 的遍历结果是一个一维数组，无法区分每一层。

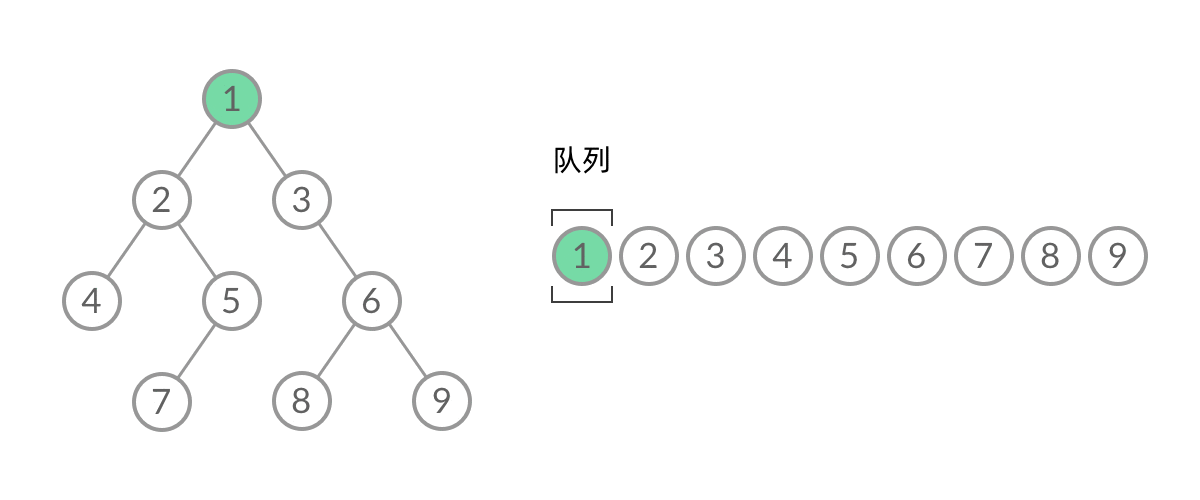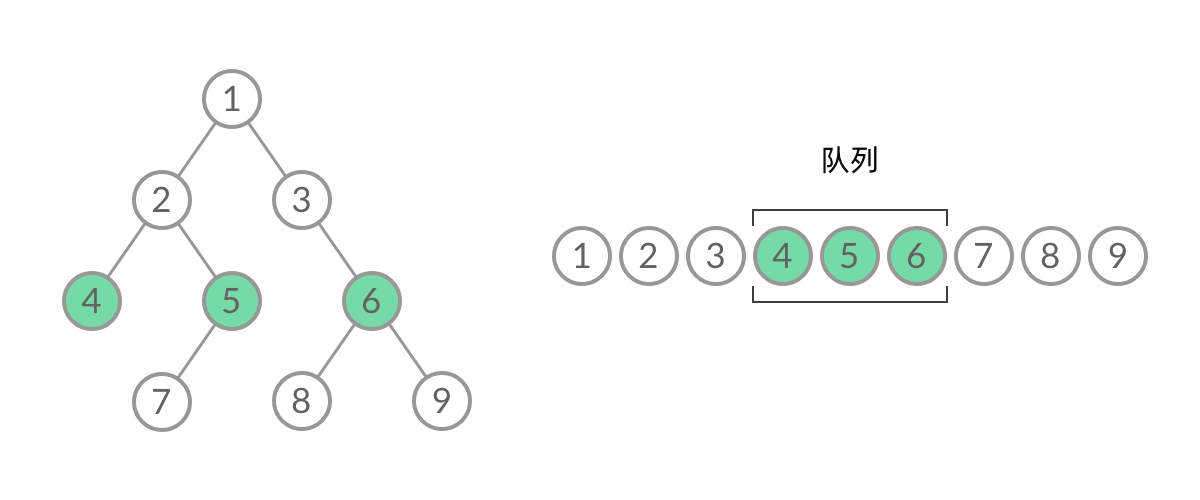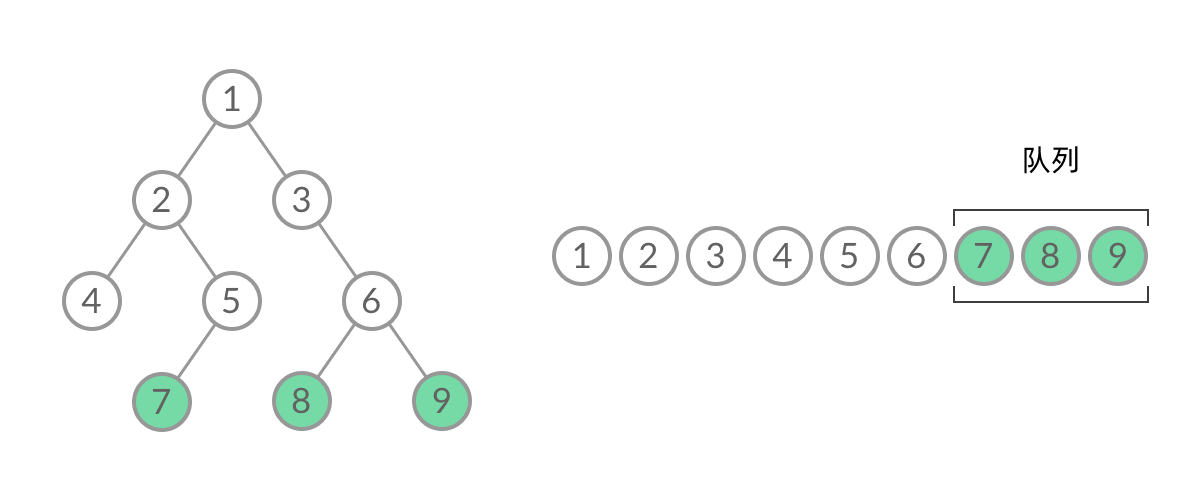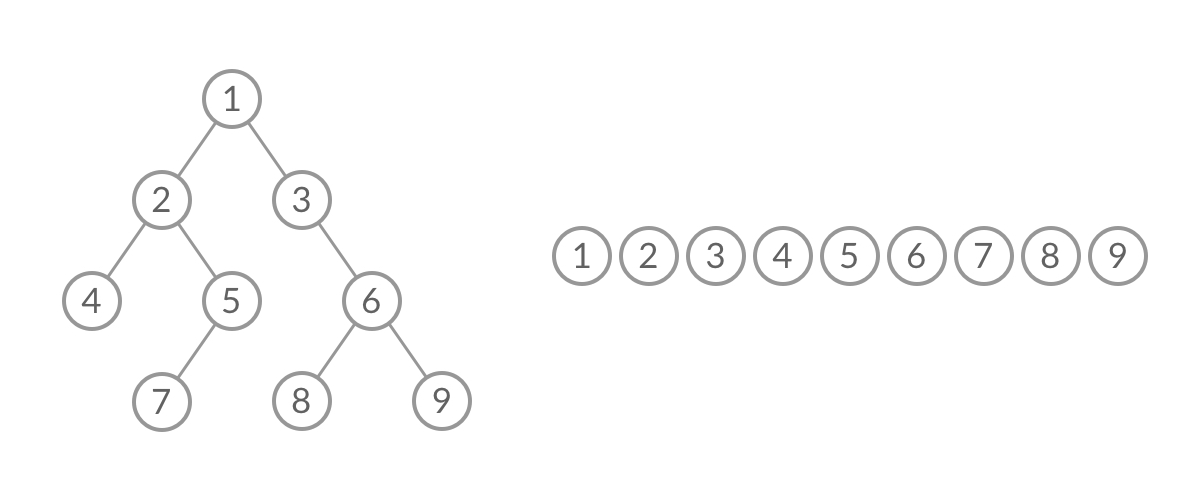
 那么，怎么给 BFS 遍历的结果分层呢？我们首先来观察一下 BFS 遍历的过程中，结点进队列和出队列的过程：

 截取 BFS 遍历过程中的某个时刻：

可以看到，此时队列中的结点是 3、4、5，分别来自第 1 层和第 2 层。这个时候，第 1 层的结点还没出完，第 2 层的结点就进来了，而且两层的结点在队列中紧挨在一起，我们 无法区分队列中的结点来自哪一层。

因此，我们需要稍微修改一下代码，在每一层遍历开始前，先记录队列中的结点数量（也就是这一层的结点数量），然后一口气处理完这一层的个结点。

// 二叉树的层序遍历 void bfs(TreeNode* root)  {     queue<TreeNode*> q;     q.push(root);     while (!q.empty())      {         int n = q.size();         for (int i = 0; i < n; i++)          {             TreeNode* node = q.front();             q.pop();             if (node->left != nullptr)              {                 q.push(node->left);             }             if (node->right != nullptr)              {                 q.push(node->right);             }         }     } }

这样，我们就将 BFS 遍历改造成了层序遍历。在遍历的过程中，结点进队列和出队列的过程为：

可以看到，在 while 循环的每一轮中，都是将当前层的所有结点出队列，再将下一层的所有结点入队列，这样就实现了层序遍历。

最终我们得到的题解代码为：

vector<vector<int>> levelOrder(TreeNode* root)  {     vector<vector<int>> res;     queue<TreeNode*> q;     if (root != nullptr)      {         q.push(root);     }     while (!q.empty())      {         int n = q.size();         vector<int> level;         for (int i = 0; i < n; i++)          {             TreeNode* node = q.front();             q.pop();             level.push_back(node->val);             if (node->left != nullptr)              {                 q.push(node->left);             }             if (node->right != nullptr)              {                 q.push(node->right);             }         }         res.push_back(level);     }     return res; } 

3.应用DFS求解的典型问题：排列组合

例题：排列组合

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

要求：

典型的DFS模板题，并且是最具代表性的例题之一排列组合类型，就是高中学的排列组合；

下面说说具体思路：首先定义几个数组，具体含义如下

vector<vector> ans; //记录答案 vector a; // 记录每次排列 map<int, int> book; //标记是否被访问

然后循环，当 nums[i] 没有被访问过时，加入数组a，并标记已经被访问，之后进行DFS递归操作，在递归结束后要释放被访问的元素，并弹出数组a。

vector<vector<int>> ans; //记录答案 vector<int> a; // 记录每次排列 map<int, int> book; //标记是否被访问 void DFS(int cur, int n, vector<int>&nums){ if(cur ==n){ ans.push_back(a); return ; } for(int i= 0; i < n; i++){ if(book[nums[i]] == 0){ a.push_back(nums[i]); book[nums[i]] = 1; DFS(cur + 1, n, nums); book[nums[i]] = 0; a.pop_back(); } } } vector<vector<int>>permute(vector<int>& nums) { int n =nums.size(); DFS(0, n,nums); returnans; }