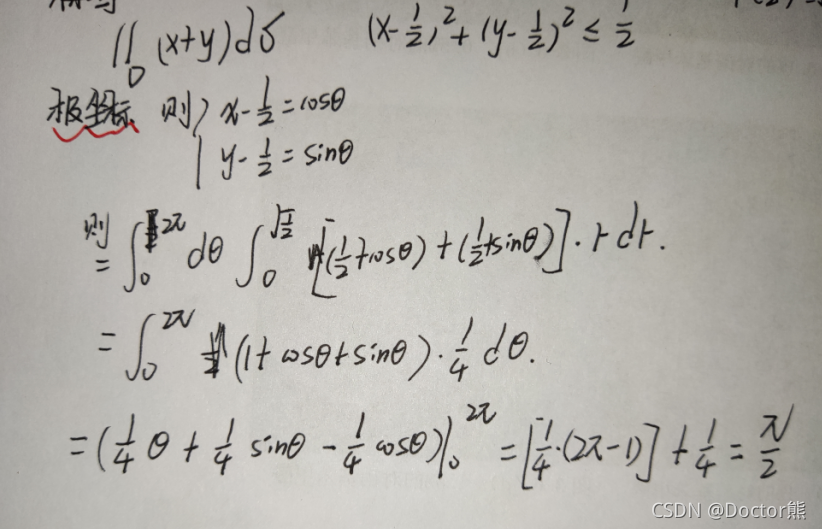大家好,欢迎来到IT知识分享网。
多元函数微积分学
一、多元函数微分学
1.1、多元函数微分学概念
连续、可偏导、可微、方向导数存在的定义
多元函数可微、可偏导、连续的关系
复合函数求偏导(链式法则)、全微分的计算
隐函数求偏导(隐函数存在定理、等式两边求导法)
1.2 方向导数、梯度的计算
物理意义:
一元函数求导数是描述在线上的点在坐标轴方向的变化率
二元函数求偏导数是描述面上的点在坐标轴方向的变化率
二元函数求方向导数描述面上的点沿着任意一个指定方向的变化率
方向导数标量,描述沿着某个方向的变化率
梯度矢量,描述多元函数变化率最大的方向
综上:沿着梯度矢量的方向,方向导数标量取最大值
计算梯度:
用来计算方向导数的梯度不能化简!
梯度函数:通过标量方程求偏导数组成的矢量函数,
某点的梯度:是一个确定的矢量,梯度函数带入点的坐标(二维或三维)
计算方向导数:
1.3 法向量、方向余弦、梯度
圆锥举例——曲面上点梯度与曲线的法向量的关系:
平面曲线:二元方程 y 2 + x 2 = 1 y^2+x^2=1 y2+x2=1
空间曲面:二元函数 f = x 2 + y 2 f=x^2+y^2 f=x2+y2,三元方程 f − y 2 − x 2 = 0 f-y^2-x^2=0 f−y2−x2=0
空间曲面求梯度 δ ( f ) δ ( x ) i + δ ( f ) δ ( y ) j \frac{\delta(f)}{\delta(x)}i+\frac{\delta(f)}{\delta(y)}j δ(x)δ(f)i+δ(y)δ(f)j
平面曲线是空间曲面的一个特例,一条等高线,垂直等高线变化最快
曲面上的点增长最快的方向,投影就是曲线的法向
知乎:梯度与面的法向量的关系
1.4 梯度(grad)、散度(div)、旋度(rot)
梯度、散度、旋度专题
1.5 多元函数极值问题
无条件极值
条件极值(拉格朗日乘数法)
限定条件的最值问题(驻点+偏导不存在+每个边界)
二、多元函数积分学:先用对称性质
2.0、积分的对称性(奇偶对称性与轮换对称性)
1.定积分、二重、三重、第一型曲线曲面积分的对称性
2.第二型曲线曲面积分的对称性
2.1、一重积分:对f(x)积分,被积区域是坐标轴
1.物理意义:
平面上的直线或曲线与坐标轴围成的面积
2.定积分的应用:
1、定积分定义
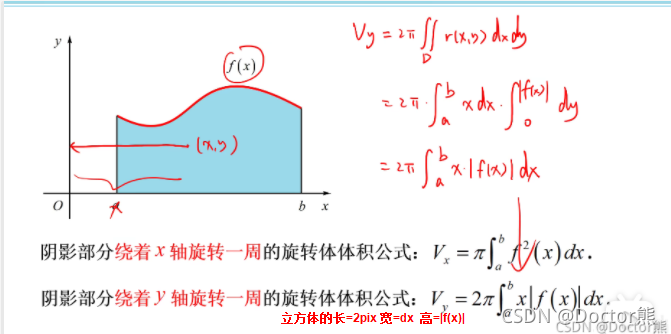
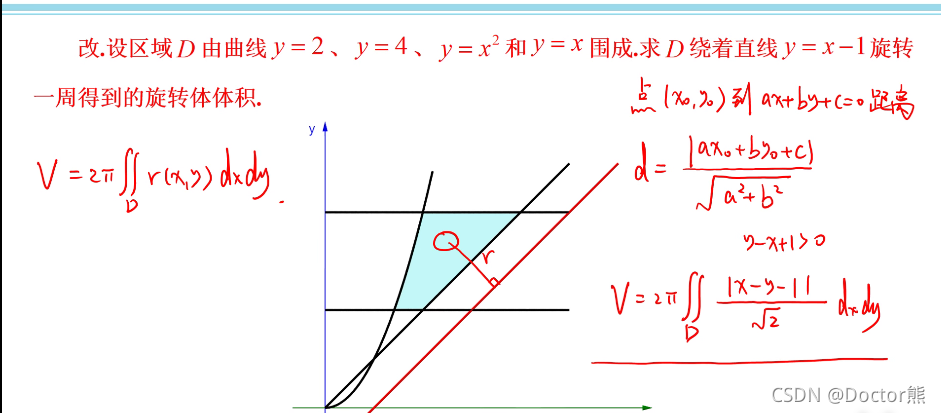
2、旋转体的体积
3、旋转体的表面积
3.重积分的应用
2.2、二重积分:对f(x,y)积分,被积区域是平面
1.计算方法:
2.物理意义
1:求密度不均匀的面的质量(f(x,y)表示密度)
2:求以曲面为顶的柱体的体积(f(x,y)表示高度)
注1:被积函数为1,就是被积区域的面积 或 高度为1的柱体体积
注2:二重积分上限大于下限,二次积分上限不一定大于下限
2.3、三重积分: 对f(x,y,z)积分,被积区域是立体
1.计算方法:先积的变量转化为后积的变量
1.直角坐标系:转换为二重积分
1)先一后二法:投影法
直角坐标系
“先一”: 上下限是x、y表达式,积分结果只含x、y
” 后二”:投影的二重积分,可能用到极坐标
柱面坐标系:先一后二的变形 ( x , y , z ) 变 成 ( θ , r , z ) (x,y,z)变成(\theta,r,z) (x,y,z)变成(θ,r,z)
“先z”:积分上下限是两个面z=z2(x,y),z=z1(x,y)用(r, θ \theta θ)
ρ 与 θ 适 用 于 g x 2 + y 2 或 者 被 积 区 域 是 柱 体 \rho与 \theta 适用于g\sqrt{x^2+y^2}或者被积区域是柱体 ρ与θ适用于gx2+y2或者被积区域是柱体
2)先二后一法:切苹果
“先二”: ( x , y , z ) 变 成 ( z , θ , r ) (x,y,z)变成(z,\theta,r) (x,y,z)变成(z,θ,r)
被积函数含x、y,可能用到极坐标上限变成含z的式子(z当成常数)
被积函数是1,”先二”就变成每层苹果的面积可以由含z的式子代替!!
“后一”:z上下限是常数的定积分
3)球面坐标系
r 与 θ 与 ϕ 适 用 于 f ( x 2 + y 2 + z 2 ) 或 者 被 积 分 区 域 是 球 体 、 锥 体 r与 \theta 与\phi 适用于f(\sqrt{x^2+y^2+z^2})或者被积分区域是球体、锥体 r与θ与ϕ适用于f(x2+y2+z2)或者被积分区域是球体、锥体
2.物理意义:
求密度不均匀的立体的质量(f(x,y,z)表示密度)
注:被积函数为1,就是被积区域的体积
2.4、第一类曲线积分:
1.定义:
对弧长的曲线积分,被积区域是无方向曲线L,微元ds
2.物理意义:
3.计算方法:ds转化为dx,再定积分
2.6、第一类曲面积分:
1.定义:
对面积的曲面积分,被积区域是无方向曲面S,微元dS
2.物理意义:
3.计算方法:ds转化为dxdy,再二重积分
曲面微分dS 乘以 曲面上一点的在z轴的方向余弦=平面微分dxdy
z=z(x,y)的方向余弦cos r通过法向量得到
2.5、第二类曲线积分:对矢量的第一类曲线积分
1.定义:
2.物理意义:
力的矢量拉着物体沿着曲线运动所做的功,将沿切向的小段位移分解到垂直的坐标轴上;同时将小段作用力也分解到垂直的坐标轴上,坐标轴分别作积分再求和得到总功。已知路径曲线方程,已知x,y两个方向的力分量或者x,y,z三个方向的力的分量,求功(有方向)
3.基本计算方法:dx与dy转化为dt,转化到定积分
4. 平面曲线的格林公式:转化到二重积分
5.空间曲线的斯托克斯公式:转化到某类曲面积分
注:
2.7、第二类曲面积分:对矢量的第一类曲面积分
1.定义
点在直线上与点在某个面上有不同的价值
1.对坐标的曲面积分,被积区域分解到坐标平面
面的两个相反的法向量对应面的不同侧
2.物理意义:
3.基本计算方法:三个化为一个(方向余弦的关系),换元转化到二重积分
注:
1.如果计算三个投影,不如利用方向余弦转换为计算一个投影
2.流量结果可正可负:
通过题干条件,确定曲面是哪一侧
根据曲面方向(法向量)与坐标轴夹角cosr,决定添加正负号
eg:
方向向量与坐标轴的三个正向都相同,则肯定为正
方向向量与坐标轴的三个正向都相反,则肯定为负
投影到xoy面,则判断这一侧的法向量朝上为正
4.高斯公式:转化到三重积分
免责声明:本站所有文章内容,图片,视频等均是来源于用户投稿和互联网及文摘转载整编而成,不代表本站观点,不承担相关法律责任。其著作权各归其原作者或其出版社所有。如发现本站有涉嫌抄袭侵权/违法违规的内容,侵犯到您的权益,请在线联系站长,一经查实,本站将立刻删除。 本文来自网络,若有侵权,请联系删除,如若转载,请注明出处:https://haidsoft.com/116972.html