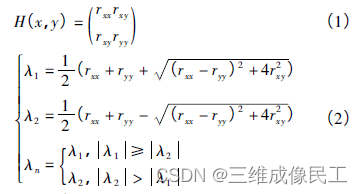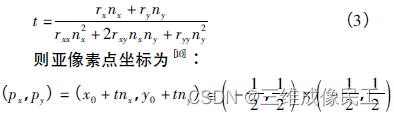【图像处理】海森矩阵（Hessian Matrix）及用例（基于Steger的中心提取_含代码）

大家好，欢迎来到IT知识分享网。

Hess矩阵是一个多元函数的二阶偏导数构成的方阵，描述了函数的局部曲率。Hess矩阵经常用在牛顿法中求多元函数的极值问题，将目标函数在某点领域内进行二阶泰勒展开，其中的二阶导数就是Hess矩阵。

海森矩阵的意义

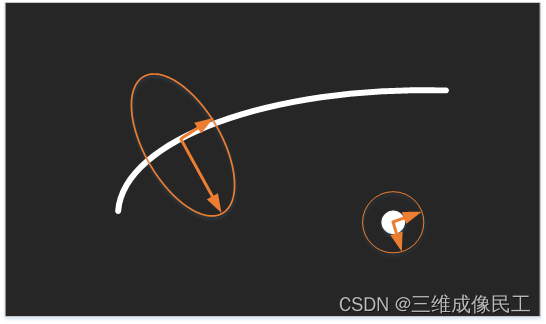
如下图所示，线条处两个特征值表示了图像在两个特征向量所指的方向上图像变化的各向异性。相似的，圆具有各项同性；线性结构越强的越是各项异性。

海森矩阵的应用（Steger算法）

其中$r_{xx}$表示图像沿x的二阶偏导，其他类似； $\lambda$则表示特征向量的长度。

Hess矩阵按照变量求二阶偏导后按顺序排列，因各二阶导连续故原函数的混合偏导数全相等，导致其是对称的，这时就可以与正负定矩阵知识联系起来。若是正负定矩阵，二阶导为系数的多项式符号确定（前提在该领域内一阶导单调），证明一阶导有零点，故配合二阶导的符号即可确定是极小还是极大。

中心点位置亚像素求解，沿着一阶梯度方向，利用下述泰勒展开获得亚像素的值，求极值让下式一阶导为0，得到偏差值距离值；
$F(x_0+t{n}_x,y_0+t{n}_y)=F(x_0,y_0)+J(x_1{)}^{\mathrm{T}}[t{n}_x,t{n}_y{]}^{\mathrm{T}}+\frac{1}{2}[tnx,tny]\ast H(x1)\ast [t{n}_x,t{n}_y{]}^{\mathrm{T}}$;

注：在求上述hessian矩阵之前，根据Steger文章中，设计高斯方差 $\sigma ⩽\frac{w}{\sqrt{3}}$；核过大，高斯分布顶部满足条件的点变多，选择中心点的精度不够，提取到的中心线会小范围的波动；核过小，中心点在二阶法线长度局部最大值处，非最小点处。

基于Steger改善算法示例代码

clc; clear; close all; tic; %% Extraction of normal binarization center based on Steger algorithm image = imread(['.\Precision\stair\8\a.bmp']); Sz = size(image); % 自动提取ROI区域阈值 Img_index = zeros(1, 245); for i = 1:Sz(1) for j = 1:Sz(2) if image(i, j) > 10 Img_index(image(i, j) - 10) = Img_index(image(i, j) - 10) + 1; end end end Img_index(245) = 0; ind_x = Img_index(1:end-1) - Img_index(2:end); ind_x = imfilter(ind_x, [1 3 6 9 10 9 6 3 1]./48, 'replicate');% ; for i = 2:245 if ind_x(i) < 10 Intensity_threshold = i + 10;%20 break; end end % choose the region of interest BC = roicolor(image, Intensity_threshold, 256); [r, c] = find(BC == 1); Range_vertical = lineboundary(r, c); global num nn = ones(1, Sz(2)); nn_sz = size(nn(Range_vertical(1, :) ~= 0)); num = sum(Range_vertical(2, :) - Range_vertical(1, :)) + nn_sz(2); %对所有ROI区域执行平滑操作 [img_filter, Index_c] = filter_gauss_1(image, Range_vertical); % Guass smoothing： Notices: sigma >= w/sqrt(3);first w = 8; DIR = [ [-1; -1], [-1; 0], [-1; 1] ... [ 0; -1], [ 0; 0], [ 0; 1]... [ 1; -1], [ 1; 0], [ 1; 1] ]; % 找到对应的中心点与线宽大小 CenterCord = zeros(2, Sz(2)); img_2filter = zeros(1, num); LineW = zeros(1, Sz(2)); for i = 2:Sz(2)-1 if i == 1110 i = 1110; end % 判断初始检索位置 y0 = (Range_vertical(2, i-1) + Range_vertical(1, i-1))/2; y1 = (Range_vertical(2, i) + Range_vertical(1, i))/2; y2 = (Range_vertical(2, i+1) + Range_vertical(1, i+1))/2; if (y0==0 || y1==0 || y2==0)|| abs(y1 - y0) > 5 || abs(y1 - y2) > 5 continue; else tempInd = find(img_filter(Index_c(i):Index_c(i+1) - 1) > 220); if length(tempInd) > 1 temp = tempInd(1) + floor(length(tempInd)/2); else [~, temp] = max(img_filter(Index_c(i):Index_c(i+1) - 1)); end tempy = Range_vertical(1, i) + temp - 1; end CenterCord(:, i) = [i; tempy]; if image(tempy, i) > 150 % 计算有限个纵向滤波 img_2f_array = Block_filter(img_filter, img_2filter, [i; tempy], Index_c, Range_vertical, gausFilter); for k = [1 2 4 5 6 8] % 开始检索([1 2 *; 4 5 6; * 8 *]') m = Index_c(i + DIR(1, k)) + tempy + DIR(2, k) - Range_vertical(1, i + DIR(1, k)); img_2filter(m) = img_2f_array(k); end [norm, lamda, t] = StegerHess(img_2f_array); if lamda(2) < 0 && abs(lamda(2))>(4 + abs(lamda(1))) W = Linewidth([i, tempy], norm, Range_vertical); % if W <= 40 LineW(i) = W; end end end end se = strel('line', 5, 0); LineWtemp = imopen(LineW, se); LineW = round(imfilter(LineWtemp, [1 3 6 9 10 9 6 3 1]./48, 'replicate')); LineW(LineW <= 5) = 0; LineW(1) = 0; % 构建高斯二阶偏导数模板 W = 5; sigma = 2.5; xxGauKernel = zeros(2*W + 1, W + 1); yyGauKernel = zeros(2*W + 1, W + 1); xyGauKernel = zeros(2*W + 1, W + 1); xGauKernel = zeros(2*W + 1, W + 1); yGauKernel = zeros(2*W + 1, W + 1); for i = -W:W for j = -W:W yyGauKernel(i + W + 1, j + W + 1) = (1 - (i*i) / (sigma*sigma))*exp(-1 * (i*i + j*j) / (2 * sigma*sigma))*(-1 / (2 * pi*sigma^4)); xxGauKernel(i + W + 1, j + W + 1) = (1 - (j*j) / (sigma*sigma))*exp(-1 * (i*i + j*j) / (2 * sigma*sigma))*(-1 / (2 * pi*sigma^4)); xyGauKernel(i + W + 1, j + W + 1) = ((i*j))*exp(-1 * (i*i + j*j) / (2 * sigma*sigma))*(1 / (2 * pi*sigma^6)); yGauKernel(i + W + 1, j + W + 1) = ( - i / (sigma*sigma))*exp(-1 * (i*i + j*j) / (2 * sigma*sigma))*(1 / (2 * pi*sigma^2)); xGauKernel(i + W + 1, j + W + 1) = ( - j / (sigma*sigma))*exp(-1 * (i*i + j*j) / (2 * sigma*sigma))*(1 / (2 * pi*sigma^2)); end end image = double(image); xxG = imfilter(image, xxGauKernel, 'replicate');% ; xyG = imfilter(image, xyGauKernel, 'replicate');% ; yyG = imfilter(image, yyGauKernel, 'replicate');% ; xG = imfilter(image, xGauKernel, 'replicate');% ; yG = imfilter(image, yGauKernel, 'replicate');% line = zeros(2, Sz(2)); % 精细中心提取 for i = 2:Sz(2)-1 if i == 37 i = 37; end y0 = (Range_vertical(2, i-1) + Range_vertical(1, i-1))/2; y1 = (Range_vertical(2, i) + Range_vertical(1, i))/2; y2 = (Range_vertical(2, i+1) + Range_vertical(1, i+1))/2; if (y0==0 || y1==0 || y2==0)|| abs(y1 - y0) > 5 || abs(y1 - y2) > 5 || LineW(i) == 0 continue; else tempx = round(CenterCord(1, i)); tempy = round(CenterCord(2, i)); if tempx == 0 && tempy == 0 continue; end mx_1order = xG(tempy, tempx); my_1order = yG(tempy, tempx); % 二阶偏导 mx2_2order = xxG(tempy, tempx); mxy_2order = xyG(tempy, tempx); my2_2order = yyG(tempy, tempx); hess = [mx2_2order mxy_2order; mxy_2order my2_2order;]; [V, D] = eig(hess); if abs(D(1, 1)) >= abs(D(2, 2)) norm = V(:, 1) ; lamda1 = D(2, 2); lamda2 = D(1, 1); else norm = V(:, 2) ; lamda1 = D(1, 1); lamda2 = D(2, 2); end lamda = [lamda1; lamda2]; t = -(norm(1)*mx_1order + norm(2)*my_1order)/ ... (norm(1)^2*mx2_2order + 2*norm(1)*norm(2)*mxy_2order + norm(2)^2*my2_2order); if lamda(2) < 0 && abs(lamda(2))>(1 + abs(lamda(1))) line(:, i) = [tempx - t*norm(1); tempy - t*norm(2)]; end end end % 检查 toc; figure; imshow(image, []); hold on plot(line(1, :), line(2, :));