树的直径——定义与求解方法

大家好，欢迎来到IT知识分享网。

如果你并没怎么接触过树，那当你看到标题时一定会感到疑惑：树又不是个圆，它哪来的直径？那就请你往下看，学习学习什么是树的直径以及树的直径的求法。

定义

我们先看看直径在圆里面有什么特点：

• 直径是圆内最长的线段。

类似的，我们对树的直径最基础的定义就是：

• 一棵树内最长的简单路径就是树的直径。

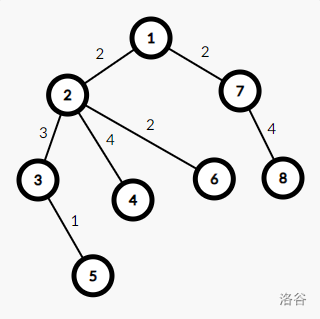
例如下面这棵树

的直径长度是 $12$。它的直径有两条：$5\to 3\to 2\to 1\to 7\to 8$ 和 $4\to 2\to 1\to 7\to 8$。

这有什么用？可以求出一些有关于树上最长路的问题。例如下面这个问题：

小 A 每天都要在树形的 X 城晨跑，小 B 负责决定路线。小 A 晨跑时不能重复经过任意一个点，但小 B 想要刁难小 A。请问小 B 应该怎么安排路线才能让小 A 跑得最远？

显然，这个问题的答案就是树的直径。

怎么求？

下面要对一棵 $n$ 个点的树求直径。

求树的直径有两种方法，它们各有优缺：

方法1：两遍 dfs

先从任意一个点开始，跑一遍 dfs，找到离这个点最远的点 $x$，再从 $x$ 开始，再跑一遍 dfs，找到离 $x$ 最远的点 $y$，$x$ 到 $y$ 就是树的一条直径。

至于为啥这样是对的……咱也不知道，咱也不敢问，反正它是对的，自信用就完了。

核心代码：

void dfs(int id,int x,int fa,long long sum){ 
   // id表示当前求的是起点还是终点，x表示当前节点，fa表示x的父亲节点，sum表示当前路径长度。  int cnt=0;//只有当前节点是叶子结点才可能是最长路径的终点，否则可以继续延伸。  for(int i=head[i];i;i=Next[i]){ 
    int y=ver[i];// 下一个节点  long long z=val[i];// 边权  if(y!=fa)dfs(id,y,x,sum+z),cnt++; } if(!cnt&&sum>Max)Max=sum,st[id]=x;// Max表示直径长度，st[1]表示直径起点，st[2]表示直径终点。  } st[0]=1; for(int i=1;i<=2;++i)Max=0,dfs(i,st[i-1],0,0);// 由主函数调用。  

方法二：树形 DP

设 $f[x][0]$ 表示以 $x$ 为根的子树中以 $x$ 为起点的最长边，$f[x][1]$ 为次长边。答案为：

max ⁡ 1 ≤ i ≤ n { f [ i ] [ 0 ] + f [ i ] [ 1 ] } \max_{1 \leq i \leq n}\{f[i][0]+f[i][1]\} 1≤i≤nmax​{
f[i][0]+f[i][1]}

注意，$f[x][1]$ 不能和 $f[x][0]$ 在同一棵子树。优先选择 $f[x][0]$。

• 运算顺序：从下往上。
• 状态转移方程：（设 $son(x)$ 表示由 $x$ 的子节点构成的集合，$W_{x,y}$ 表示连接 $x$ 和 $y$ 的边的边权）

f [ x ] [ 0 ] = max ⁡ y ∈ s o n ( x ) { f [ x ] [ 0 ] + W x , y } f[x][0]=\max_{y \in son(x)}\{f[x][0]+W_{x,y}\} f[x][0]=y∈son(x)max​{
f[x][0]+Wx,y​}

假设上面的方程最终值为 $f[d][0]+W_{x,d}$，则：

f [ x ] [ 1 ] = max ⁡ y ∈ s o n ( x ) , y ≠ d { f [ x ] [ 0 ] + W x , y } f[x][1]=\max_{y \in son(x),y \not=d}\{f[x][0]+W_{x,y}\} f[x][1]=y∈son(x),y=dmax​{
f[x][0]+Wx,y​}

核心代码：

void dp(int x,int fa){ 
   // x表示当前节点，fa表示x的父亲节点。  int d=0;// f[x][0]继承了哪个节点  for(int i=head[x];i;i=Next[i]){ 
    int y=ver[i];// 子节点 long long z=val[i];// 边权  if(y!=fa){ 
    dp(y,x); if(f[y][0]+val[i]>f[x][0])f[x][0]=f[y][0]+z,d=y; } } for(int i=head[x];i;i=Next[i]){ 
    int y=ver[i];// 子节点  long long z=val[i];// 边权  if(y!=fa&&y!=d)f[x][1]=max(f[x][1],f[y][0]+z); } Max=max(Max,f[x][0]+f[x][1]); } dp(1,0);// 由主函数调用。  

例题：

总结：树的直径指的是一棵树上最长的简单路径，通常用于解决树上最长路径问题。而直径的两种求法各有优缺，有些时候要结合着用。